Esercizi sul moto circolare uniforme
Esercizi online e gratuiti sul moto circolare uniforme
In questa sezione del sito sono proposti esercizi sul moto circolare uniforme.
La raccolta degli esercizi sul moto circolare uniforme di seguito proposta è rivolta sia agli studenti universitari delle facoltà scientifiche che agli studenti di licei ed istituti tecnici.
Prima di procedere allo svolgimento degli esercizi sul moto circolare uniforme, presentiamo le nozioni di base e le formule fondamentali per affrontare questa categoria di problemi.
Il moto circolare uniforme è il moto di un corpo che descrive una traiettoria circolare percorsa con velocità costante in modulo.
Tale velocità si definisce "velocità tangenziale" e rappresenta la lunghezza di circonferenza percorsa durante il periodo di rotazione T:
V = lunghezza circonferenza / periodo = 2·π·R/T
in cui
π = 3,14
R è il raggio della circonferenza
T è il periodo di rotazione, ovvero l'intervallo di tempo necessario a compiere un giro completo.
Si definisce velocità angolare invece il rapporto tra l'angolo al centro spazzato e il tempo impiegato a spazzarlo:
ω = 2·π/T
Si dice frequenza del moto l'indicazione di quanti giri completi si sono percorsi in 1 secondo, ed è pari all'inverso del periodo :
f = 1/T
L'unità di misura della frequenza è l'hertz [Hz].
L'accelerazione centripeta è invece definita come
ac = V2/R
Valgono pertanto le seguenti relazioni:
V = ω · R
Ω = V/R
ac = ω2 R
Chimica-online.it inoltre ti mette a disposizione anche una calcolatrice scientifica e un formulario di fisica.
Ti potrebbe anche interessare: formule del moto circolare uniforme.
Esercizi sul moto circolare uniforme
Di seguito gli esercizi sul moto circolare uniforme elencati secondo un ordine crescente di difficoltà.
Livello di difficoltà medio-basso
1.
Un punto materiale si muove lungo una circonferenza il cui raggio misura 15 m con una velocità tangenziale costante pari a 25 m/s.
Calcolare il periodo e la frequenza del moto, l'accelerazione centripeta, e la velocità angolare.
Lo svolgimento dell'esercizio lo trovi qui: calcolo del periodo e della frequenza in un moto circolare uniforme.
2.
Un satellite artificiale in orbita attorno alla Terra è soggetto ad un'accelerazione centripeta di 9,8 m/s2.
Qual è la velocità tangenziale ed il periodo dell'orbita?
PS Approssimare il raggio dell'orbita a 6371 km (pari al valore del raggio della Terra)
La soluzione dell'esercizio la trovi qui: calcolo della velocità tangenziale.
3.
Calcolare velocità tangenziale ed accelerazione centripeta di un elettrone che ruota attorno al nucleo di un atomo di idrogeno, assumendo che l'orbita sia circolare di raggio 5 · 10-11 m e che il periodo sia pari a 1,5 · 10-16 s.
Calcolare infine la velocità angolare.
La soluzione la trovi qui: esercizio sul calcolo della velocità angolare.
4.
Un corpo si muove di moto circolare uniforme lungo una circonferenza lunga 37,68 m, compiendo 1800 giri al minuto.
Calcolare il periodo, la velocità angolare e quale angolo descrive il corpo in 1,5 s.
Lo svolgimento dell'esercizio lo trovi qui: calcolo del periodo in un moto circolare uniforme.
5.
Lungo la sua orbita attorno al Sole, la Terra mantiene una distanza media dall'astro di 1,50∙1011 m.
Sapendo che il periodo di rivoluzione della Terra intorno al Sole, cioè l'anno è composto da 365,25 giorni, determinare la velocità media di rotazione della Terra intorno al Sole.
Si consideri che la Terra ruoti attorno al Sole con moto circolare uniforme.
Lo svolgimento dell'esercizio lo trovi qui: velocità di rotazione della Terra attorno al Sole.
6.
Determina la frequenza e la velocità angolare delle lancette dei secondi, dei minuti e delle ore di un orologio.
Lo svolgimento dell'esercizio lo trovi qui: calcolo della velocità angolare in un moto circolare uniforme.
7.
Le pale di una turbina sono lunghe 6,7 m e ruotano con velocità angolare costante.
Sapendo che la frequenza di rotazione misurata vale 4,5·102 giri /min calcolare la velocità tangenziale degli estremi di una pala e di un punto di una pala posto a 3,5 m dall'asse di rotazione.
Confronta i due valori e commentane i risultati.
Calcola infine il rapporto tra l'accelerazione centripeta della punta della pala con quella del punto che si trova a 3,5 m dall'asse di rotazione.
Lo svolgimento dell'esercizio lo trovi qui: pale di una turbina che ruotano di moto circolare uniforme.
8.
Calcolare Il modulo della velocità tangenziale della Terra nel suo moto di rivoluzione attorno al Sole sapendo che il raggio della sua orbita attorno all'astro è pari a 1,49 · 1011 m.
Lo svolgimento dell'esercizio lo trovi qui: velocità tangenziale della Terra.
9.
Un punto materiale si sta muovendo di moto circolare uniforme ed ha percorso un angolo di 30° in ⅙ s.
Determinare velocità angolare, periodo del moto e frequenza.
La soluzione dell'esercizio la trovi qui: calcolo della frequenza in un moto circolare uniforme.
10.
Un corpo puntiforme di massa m è sospeso tramite un filo di lunghezza L e sta ruotando di moto circolare uniforme lungo una circonferenza di raggio r.
Sapendo che il filo risulta inclinato di un angolo α rispetto alla verticale determinare la velocità del corpo e la tensione del filo.
La soluzione dell'esercizio la trovi qui: massa sospesa ad un filo che ruota di moto circolare uniforme.
11.
L'addestramento degli astronauti destinati ai viaggi spaziali verso la stazione orbitante prevedono delle simulazioni di aumento dell'accelerazione di gravità.
Ad esempio, durante la fase di discesa del velivolo sulla Terra proveniente dallo spazio, a causa della presenza dell'atmosfera terrestre, la velocità può passare bruscamente anche da 8000 m/s a 300 m/s.
Gli astronauti pertanto potrebbero essere sottoposti ad accelerazioni di gravità fino a 8g.
Per simulare questa situazione critica, si utilizza un braccio rotante di circa 18 m posto in velocità costante e al cui estremo è presente un fissaggio a cui risulta ancorato l'astronauta.
Determinare a che velocità deve ruotare il braccio affinché; la simulazione avvenga correttamente e quanti giri compie in un minuto.
La soluzione dell'esercizio la trovi qui: esercizio sulla velocità tangenziale.
Livello di difficoltà medio-alto
12.
La velocità tangenziale di un punto di una ruota a distanza 20 cm dall'asse di rotazione di un'automobile in moto è 15 m/s.
Calcolare il diametro della ruota, sapendo che la velocità dell'automobile è 108 km/h.
Lo svolgimento dell'esercizio lo trovi qui: applicazione della velocità tangenziale.
13.
Calcolare quanti giri al minuto deve compiere una piattaforma circolare di raggio R = 3 m affinché un punto del bordo sia sottoposto ad un'accelerazione pari a 10·g.
Lo svolgimento dell'esercizio lo trovi qui: calcolo del numero di giri al minuto.
14.
L'accelerazione centripeta a cui è soggetto un corpo presente all'equatore è pari a 3,0 cm/s2.
Di quale fattore dovrebbe crescere la velocità di rotazione della Terra, perché per trattenere un corpo all'equatore fosse necessaria un'accelerazione centripeta pari a g?
Si sappia che il raggio della Terra è un valore noto e costante e vale: R = 6,4 ·106 m
Lo svolgimento dell'esercizio lo trovi qui: applicazione della accelerazione centripeda.
15.
Due corpi A e B si muovono su due circonferenze concentriche di raggio RA=1m e RB=2m .
All'istante iniziale sono sull'asse y ed hanno VA=1,1 m/s e VB=1,6 m/s.
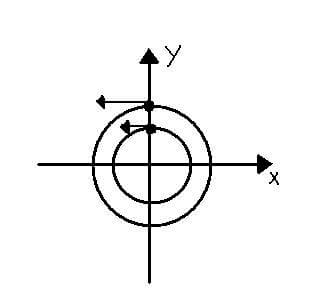
Si trovi quando si ritrovano allineati e in quale posizione.
Lo svolgimento dell'esercizio lo trovi qui: corpi che si muovono su due circonferenze concentriche.
Livello di difficoltà: alto
16.
In una pista circolare di go-kart di raggio R = 40 m due partecipanti si esibiscono in una gara di inseguimento.
Essi partono allo stesso istante posizionati ai due estremi del diametro orizzontale della pista, il primo con velocità VA e l'altro con velocità VB = 40 km/h.
Trovare il valore di V1 affinché il primo partecipante raggiunga il secondo dopo che questo ha percorso 2,5 giri di pista e calcolare il tempo necessario.
Lo svolgimento dell'esercizio lo trovi qui: corpi che si muovono di moto circolare uniforme sfasati tra loro.
17.
Su una circonferenza di raggio 3 m si muovono due punti che si incontrano ogni 20 s se viaggiano nello stesso verso, mentre si incontrano ogni 4 s se si muovono in verso opposto.
Supponendo che il moto dei due corpi sia circolare uniforme, determinare il modulo delle due velocità dei due corpi.
Lo svolgimento dell'esercizio lo trovi qui: punti che si muovono di moto circolare uniforme lungo la stessa circonferenza di raggio.
Studia con noi