Satelliti
Moto dei satelliti
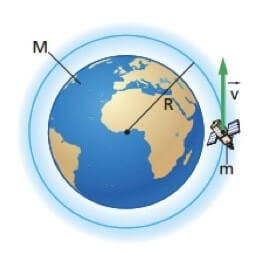
Un satellite è un corpo di massa e dimensioni inferiori che ruota intorno ad un pianeta principale.
Sono satelliti la Luna (satellite naturale) o i satelliti artificiali per la Terra, le lune di Giove, quelle di Saturno ecc.
Nel caso di satelliti geostazionari si ci riferisce al pianeta Terra.
La parola geostazionaria in sostanza vuol dire che il satellite ruota intorno alla Terra in modo tale che per un osservatore sulla superficie, il satellite appare fermo.
Questo può accadere solo se il satellite si muove in modo sincrono con la Terra.
La velocità e il periodo dei satelliti
Consideriamo un satellite in orbita attorno alla Terra.
Sappiamo che possiamo considerare con buona approssimazione la sua orbita come circolare.
Dal secondo principio della dinamica, possiamo affermare che il satellite ruota in quanto la risultante di tutte le forze che agiscono sul satellite è pari alla forza centripeta.
L'unica forza ad agire sul corpo in orbita è la forza di gravitazione.
Per cui imponiamo che:
Fg = Fc
per cui:
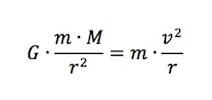
in cui:
- m è la massa del satellite;
- M è la massa della Terra;
- r la distanza del satellite dal centro della Terra;
- v la velocità tangenziale del satellite lungo la sua orbita circolare.
Dalla precedente relazione possiamo semplificare la massa m del satellite e la distanza r:
G ∙ M / r = v2
Da cui:
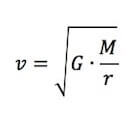
che rappresenta la formula necessaria al calcolo della velocità di un satellite in orbita.
Ci si accorge che aumentando la distanza dal centro della Terra la velocità decresce, per cui i satelliti più sono posti in orbite lontane dal centro della Terra più lenti saranno.
Per quanto riguarda invece il calcolo del periodo dell'orbita di un satellite, ricordando che in un moto circolare uniforme la velocità tangenziale è definita come la lunghezza orbitale fratto il periodo:
v = 2 ∙ π ∙ r / T
Allora il periodo sarà:
T = 2 ∙ π ∙ r / v
Sostituendo a v l'espressione prima ricavata:
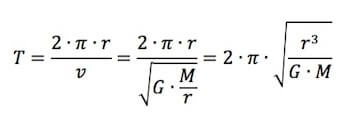
Quindi:
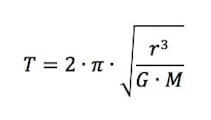
Per cui si conclude che i satelliti posti in orbite più lontane dal centro della Terra impiegano periodi di tempo maggiori.
Satelliti geostazionari
Alcuni importanti satelliti artificiali che sono posti in rotazione attorno alla Terra, hanno la necessita di ruotare in maniera solidale con il nostro pianeta, ovvero devono stazionare sempre sopra lo stesso punto posto sull'equatore durante la loro orbita.
È come se essi ruotassero fissi con la Terra; tale necessità si rileva ad esempio nei satelliti meteorologici o per quelli delle telecomunicazioni.
Affinché ciò accada è necessario che il periodo di rotazione del satellite intorno alla Terra sia lo stesso che il nostro pianeta impiega per una rotazione completa attorno al proprio asse ovvero 24 ore.
Per cui un satellite geostazionario sembra apparentemente fermo rispetto ad un punto sulla superficie terrestre.
Esercizio
Sapendo che la costante di gravitazione universale vale G = 6,67 ∙ 10−11 N ∙ m² / kg² e che la massa della Terra è M = 5,97 ∙ 1024 kg, si determini il raggio medio dell'orbita di un satellite geostazionario.
Lo svolgimento dell'esercizio lo trovi qui: raggio medio dell'orbita di un satellite geostazionario.
Link correlati:
7 curiosità sugli anelli di Saturno
Studia con noi