Massa sospesa ad un filo che ruota di moto circolare uniforme
Esercizio riguardante una massa sospesa ad un filo che ruota di moto circolare uniforme
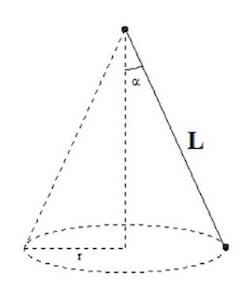
Un corpo puntiforme di massa m è sospeso tramite un filo di lunghezza L e sta ruotando di moto circolare uniforme lungo una circonferenza di raggio r.
Sapendo che il filo risulta inclinato di un angolo α rispetto alla verticale determinare la velocità del corpo e la tensione del filo.
Svolgimento dell'esercizio
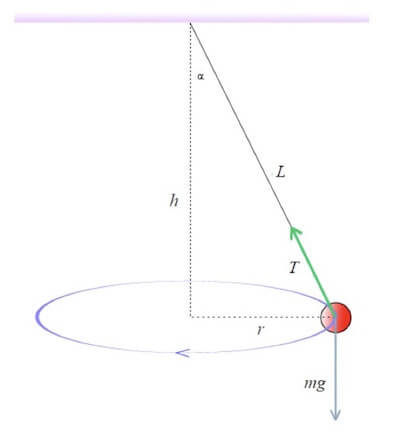
L'esercizio propone il caso di una massa m che è appesa ad un filo e che sta ruotando di moto circolare uniforme.
Sapendo che il filo è inclinato rispetto alla verticale di un angolo α, si vuole determinare la velocità del corpo e la tensione del filo.
Il sistema può essere rappresentato nel seguente modo:
Consideriamo il seguente sistema di assi cartesiani:
Le forze che agiscono sul corpo sono la tensione T della fune orientata lungo il filo e rivolta verso il punto in cui è appeso il filo e la forza peso diretta verso il basso; la risultante sarà la forza centripeta diretta verso il centro.
La tensione dunque avrà due componenti una lungo x e una lungo y:
Per cui il diagramma di corpo libero risulterà essere:
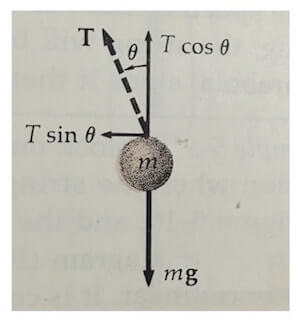
Scriviamo la seconda legge di Newton sia per l'asse x sia per l'asse y.
Sull'asse y non c'è moto, dunque l'accelerazione è nulla. Cioè le forze si bilanciano; per cui:
T∙cosα - m∙g = 0
Invece sull'asse x l'unica forza presente è la componente x della tensione la cui risultante è appunto la forza centripeta che permette il moto circolare:
T∙senα = m ∙ ac = m ∙ v2 / r
Dalla prima ricaviamo T:
T = m∙g / cosα
Che sostituita nella seconda:
T∙senα = m ∙ v2 / r
m∙g / cosα ∙senα = m ∙ v2 / r
Semplificando m e tenendo conto che senα/cosα = tgα:
tgα ∙ g = v2 / r
Ricaviamo v:
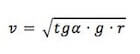
I casi limiti sono per α = 0 non esiste più il pendolo conico in quanto tg0 = 0 il corpo sta fermo e per α = 90° pendolo conico degenere.
Studia con noi