Corpi che si muovono su due circonferenze concentriche
Esercizio su corpi che si muovono su due circonferenze concentriche
Due corpi A e B si muovono su due circonferenze concentriche di raggio RA=1m e RB=2m .
All'istante iniziale sono sull'asse y ed hanno VA=1,1 m/s e VB=1,6 m/s.
Si trovi quando si ritrovano allineati e in quale posizione.
Svolgimento
Il problema propone la situazione di due punti che si muovono di moto circolare uniforme su due circonferenze concentriche, cioè due circonferenze una contenuta nell'altra con il medesimo centro.
Disegniamo pertanto un sistema di assi coordinati x ed y.
I due punti partono allineati sull'asse verticale.
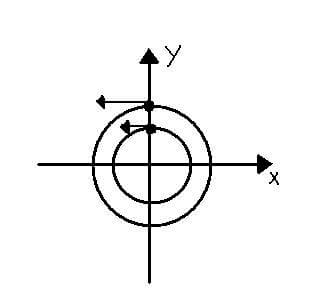
Calcoliamo le velocità angolari dei due punti.
ωA = VA/RA = 1,1/1 = 1,1 rad/s
ωB = VB/RB = 1,6/2 = 0,8 rad/s
I due angoli descritti dai due punti A e B devono essere tali per cui:
αA - αB = 2·π
Infatti essendo i due punti allineati, la distanza angolare da compiere partendo da un punto per arrivare all'altro è proprio un angolo giro quindi 2·π, inoltre ricordando che
αA = ωA·t
e
αB = ωB·t
I due punti saranno riallineati solo quando
ωA·t - ωB·t = 2·π
raccogliamo t
(ωA - ωB) · t = 2·π
Da cui
t = 2·π / (ωA - ωB) = 2·3,14 /(1,1 - 0,8) = 20,93 s
L'angolo percorso sarà pari a:
αA = ωA·t = 1,1 · 20,93 = 23,02 rad
corrispondenti a un numero di giri pari a:
n = 23,02/(2·π) = 3,67 giri
αB = ωB·t = 0,8 · 20,93 = 16,74 rad
corrispondenti a un numero di giri pari a:
n = 16,74/(2·π) = 2,67 giri
Quindi i due punti si ritrovano riallineati dopo 20,93 s dalla loro partenza e dopo aver percorso rispettivamente 3,67 giri e 2,67 giri.
Link correlati:
Quali sono le formule del moto circolare uniforme?
Studia con noi