Reattanza
Che cos'è la reattanza?
I tre elementi che di base possono essere presenti in un circuito sono la resistenza R, il condensatore C e l'induttanza L. Riassumiamo in questa tabella le principali proprietà e caratteristiche:
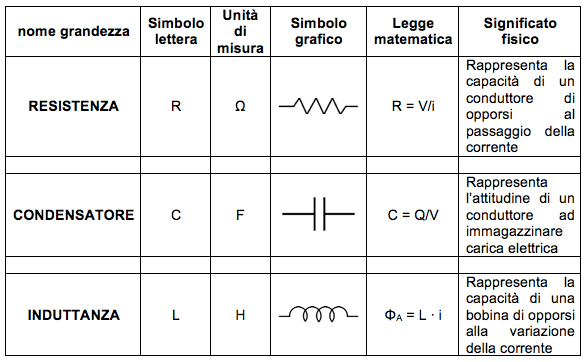
I tre elementi circuitali in corrente continua
Vediamo come si comportano i tre elementi che abbiamo appena elencato quando essi sono collegati ad un generatore di tensione continua cioè che eroga una tensione costante nel tempo ed il cui simbolo grafico è
Nel caso della resistenza, in essa scorre istantaneamente una volta chiuso il circuito una corrente costante ed il grafico corrente - tensione è una retta passante per l'origine seguendo la prima legge di Ohm (conduttori Ohmici)
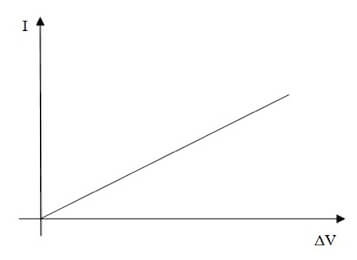
La resistenza R di un conduttore inoltre dipende dalle caratteristiche geometriche del conduttore e dalla natura del materiale del conduttore. In particolare la seconda legge di Ohm chiarisce che la resistenza R di un conduttore è pari al prodotto del coefficiente di resistività ρ che dipende dal materiale e dalla temperatura, dalla lunghezza L del conduttore e dalla sua sezione S secondo la formula:
R = ρ ∙ L / S
Nel caso di un condensatore inizialmente scarico una volta chiuso il circuito c'è un brevissimo ed istantaneo regime di transitorio in cui circola corrente grazie al fatto che le armature si stanno caricando ed una volta esaurito questo brevissimo transitorio quindi il condensatore si comporta come un circuito aperto che non fa circolare corrente in quanto saturo di carica elettrica pari al prodotto della capacità C per la differenza di potenziale tra le sue armature Q = C∙ V.
Il transitorio di un circuito puramente capacitivo, cioè comprendente solo un condensatore, è idealmente tendente a zero e la tensione tra le armatura del condensatore passa istantaneamente al suo valore a regime.
Nella realtà bisogna sempre considerare anche una piccola resistenza dovuta agli stessi fili di conduzione e quindi nella pratica si osserverà un comportamento della corrente di questo genere come quella di un circuito RC:
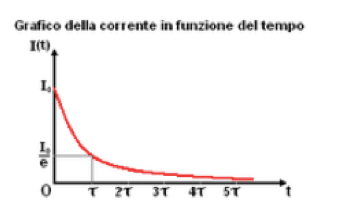
La capacità C di un condensatore inoltre dipende dalle sue caratteristiche geometriche e fisica e dall'eventuale dielettrico posto tra le sue armature.
In particolare è direttamente proporzionale alla costante dielettrica relativa del materiale isolante posto tra le armature (per il vuoto vale 1) ed alla superficie S delle armature del condensatore mentre è inversamente proporzionale alla loro distanza d:
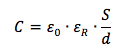
Infine nel caso di un'induttanza collegata in continua si osserverà nel caso ideale a regime un corto circuito in quanto la resistenza della bobina è considerata nulla, cioè per qualsiasi valore della corrente la tensione ai suoi capi è nulla e all'interno della bobina si manifesterà un campo magnetico uniforme, che abbiamo analizzato dettagliatamente quando abbiamo parlato del solenoide. Quando la corrente varia il flusso del campo magnetico auto concatenato è istante per istante pari al prodotto dell'induttanza L per la corrente i.
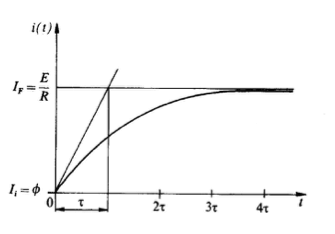
Nella pratica però anche in questo caso come per il circuito puramente capacitivo visto prima i fili assumono sempre un minimo di resistenza elettrica e quindi il comportamento della corrente è come quella di un circuito RL in cui dopo un breve transitorio si stabilizza in un certo valore a regime. La salita della corrente in particolare è ostacolata dalle correnti autoindotte nelle bobine per la legge di Faraday Neumann Lenz.
L'induttanza L di una bobina dipende dall'eventuale presenza del nucleo ferromagnetico al suo interno e quindi dalla sua permeabilità magnetica relativa μR, dal numero di avvolgimenti N che compongono la bobina, dalla sua lunghezza L e dalla sua sezione S secondo la formula:
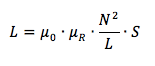
I tre elementi circuitali in corrente alternata
Vediamo adesso come si comportano resistenza, condensatore e induttanza quando essi sono collegati ad un generatore di tensione alternata cioè che eroga una tensione variabile nel tempo secondo un andamento sinusoidale ad una certa frequenza f ed il cui simbolo grafico è
Tensione e corrente oscillano secondo leggi matematiche sinusoidale eventualmente sfasate tra di loro ma con la stessa frequenza f e pulsazione ω:
V(t) = V0 ∙ sen(ω ∙ t)
i(t) = i0 ∙ sen(ω ∙ t + φ)
in cui φ è l'eventuale fase di sfasamento tra corrente e tensione.
Nel caso ideale, la resistenza si comporta allo stesso modo del caso continuo solo che i valori di tensione e corrente misurati ai suoi capi hanno un andamento variabile così come la fem erogata dal generatore. Tensione e corrente hanno sfasamento nullo quindi φ=0
Il condensatore e l'induttore invece in alternata non si comportano più come nel caso continuo ma bisogna introdurre il concetto di reattanza. La reattanza fa riferimento al fatto che condensatore e induttore non si comportano in alternata così come si comportano in continua ma "reagiscono" in maniera diversa.
In particolare nel caso del condensatore la corrente oscillerà in anticipo di un quarto di periodo (φ=+π/2) rispetto alla tensione mentre nell'induttore la corrente oscillerà in ritardo di un quarto di periodo (φ=-π/2) rispetto alla tensione.
Quindi essendo sfasate tra di loro tensione e corrente si definisce reattanza il rapporto tra la tensione massima e la corrente massima nel condensatore o nell'induttore e rappresenta l'opposizione data da una pura induttanza o da una pura capacità al passaggio della corrente alternata. Il simbolo con cui si indica è la Χ e l'unità di misura è l'ohm Ω.
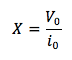
Reattanza capacitiva
La reattanza riferita al condensatore è detta reattanza capacitiva ed è pari al reciproco del prodotto della pulsazione ω con cui oscillano sia la fem sia la corrente per la capacità C:
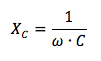
La pulsazione ω con cui oscilla la fem alternata è pari a 2 ∙π ∙ f in cui f è la frequenza di oscillazione. Questo significa che se la frequenza con cui oscilla la tensione aumenta allora anche la pulsazione aumenta e quindi la reattanza capacitiva diminuisce ciò vuol dire che il condensatore riesce ad opporsi di meno al passaggio della corrente alternata.
Così come se aumenta la capacità vuol dire che è aumentata la capacità di immagazzinare carica elettrica e dunque il processo di carica e scarica può avvenire più agevolmente diminuendo dunque anche in questo caso la reattanza capacitiva.
La reattanza capacitiva di un condensatore è dunque inversamente proporzionale alla pulsazione ed alla capacità del condensatore.
Reattanza induttiva
La reattanza riferita all'induttanza è detta reattanza induttiva ed è pari al prodotto della pulsazione ω per l'induttanza L:
![]()
La pulsazione ω con cui oscilla la fem alternata è pari a 2 ∙π ∙ f in cui f è la frequenza di oscillazione.
Questo significa che se la frequenza con cui oscilla la tensione aumenta allora anche la pulsazione aumenta e quindi la reattanza induttiva aumenterà, in quanto la corrente varia maggiormente, e per la legge di Faraday Neumann Lenz l'induttanza si opporrà maggiormente alla variazione di essa. La reattanza induttiva è dunque direttamente proporzionale sia alla pulsazione sia all'induttanza L.
Impedenza di un circuito
Quando siamo in presenza di un circuito complesso contenente contemporaneamente resistenze, capacità e induttanze, la reattanza capacitiva e quella induttiva possono essere riscritte a partire da una grandezza complessiva che le contiene detta impedenza del circuito, indicata con la lettera Z e misurata in Ohm.
L'impedenza Z rappresenta dunque la reattanza complessiva di un circuito e si definisce come il rapporto tra la tensione massima alternata e la corrente massima alternata nel circuito (così come la reattanza):
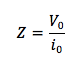
In particolare per un circuito RLC, contenente cioè una resistenza, un condensatore ed un induttore posti in serie l'impedenza vale:
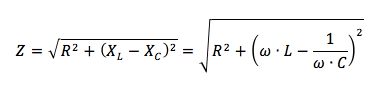
Nel caso particolare in cui non ci siano capacità ed induttanze e quindi non siano presenti i due termini XC e XL allora l'impedenza diventa semplicemente la resistenza. Allo stesso modo se XC = XL l'impedenza sarà ancora rappresentata semplicemente dalla resistenza e quindi l'impedenza assumerà il suo valore minimo pari a R.
La condizione XC = XL viene dette condizione di risonanza e corrisponde al valore minimo assunto dall'impedenza in un circuito RLC.
Per trovare la pulsazione ω in cui si verifica questa condizione:
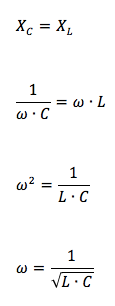
Link correlati:
Che cos'è la suscettanza?
Calcolo della reattanza di un circuito LC
Calcolo della risonanza di un circuito RLC
Esercizio svolto sul teorema di Thevenin
Qual è l'unità di misura della resistenza elettrica?
Che cosa sono i superconduttori?
Cosa afferma la seconda legge di Ohm?
Che cos'è la conduttanza elettrica?
Studia con noi