Seconda legge di Ohm
Cosa afferma la seconda legge di Ohm?
Quando abbiamo parlato della prima legge di Ohm abbiamo visto come la resistenza elettrica del conduttore fosse pari a un rapporto costante (in regime stazionario) tra la ddp applicata ai suoi capi e l'intensità di corrente che lo attraversa:
R = ΔV / i
Visto che tale rapporto è costante, da che cosa dipende allora la resistenza di un conduttore?
La resistenza elettrica di un materiale dipende dalle caratteristiche fisiche del conduttore e dal materiale stesso di cui è composto cioè dalla sua natura.
Enunciato della seconda legge di Ohm
In particolare la seconda legge di Ohm afferma che la resistenza R di un conduttore è pari a:
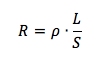
in cui:
- ρ è il coefficiente di resistività tipico di ogni materiale e si misura in Ω∙m;
- L è la lunghezza del conduttore;
- S la sua sezione in m2.
Dunque si può affermare correttamente che la resistenza elettrica di un conduttore è direttamente proporzionale alla lunghezza del conduttore ed inversamente proporzionale alla sua sezione.
Resistenza e temperatura
La resistenza di un conduttore è costante se la temperatura a cui viene mantenuto è costante.
Infatti il coefficiente di resistività ρ è una funzione della temperatura.
Solitamente viene fornito il coefficiente di resistività a 20°C (293 K) (temperatura ambiente); di seguito riportiamo i valori della resistività di alcuni materiali:
resistività dell'alluminio = 2,75∙10-8 Ω∙m
resistività del nichel = 6,993∙10-8 Ω∙m
resistività del rame = 1,68∙10-8 Ω∙m
resistività del ferro = 10,04∙10-8 Ω∙m
resistività della costantana = 49∙10-8 Ω∙m
Alcuni isolanti come il vetro sono dotati di valori di resistività elevatissimi e di conseguenza risultano elevati i valori delle resistenze rendendo praticamente nulla la corrente che li attraversa.
Ad un primo approccio è corretto pensare che se la temperatura aumenta, aumenteranno anche le vibrazioni molecolari del conduttore stesso e dunque sarà più probabile che gli elettroni di conduzione vengano maggiormente ostacolati nel loro percorso all'interno dal conduttore dagli urti con gli elettroni del conduttore. Questo porta ad un aumento della resistenza.
Viceversa temperature più basse tendono a far diminuire la resistenza del conduttore.
Legame tra resistività e temperatura
Il coefficiente di resistività ρ che compare nella seconda legge di Ohm ha una forte dipendenza dalla temperatura a cui si trova la resistenza.
Il coefficiente di resistività è funzione della temperatura secondo questa relazione:
ρ(T) = ρ293 [1 + α ∙ ΔT]
Il parametro α (unità di misura K-1) si dice coefficiente termico o di variazione della resistività e determina di quanto la resistività varia in funzione della temperatura.
ρ293 è il coefficiente di resistività a 293 K cioè a temperatura ambiente (20°C) mentre ΔT è la differenza di temperatura da esprimersi in Kelvin (o Celsius perché sappiamo che la differenza tra due temperature è equivalente sia se espressa in K sia in °C in quanto entrambe scale centigrade).
In generale la formula che consente di calcolare il coefficiente di resistività di un materiale è della forma:
ρ(T) = ρ0 ∙ [1 + α ∙ (T - T0)]
in cui ρ(T) è la resistività a temperatura T e ρ0 è la resistività alla temperatura T0.
Il coefficiente α è definito come:
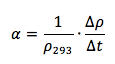
essendo Δρ la variazione di resistività nell'intervallo di temperatura Δt.
La tabella con i coefficienti termici per i principali materiali è la seguente:
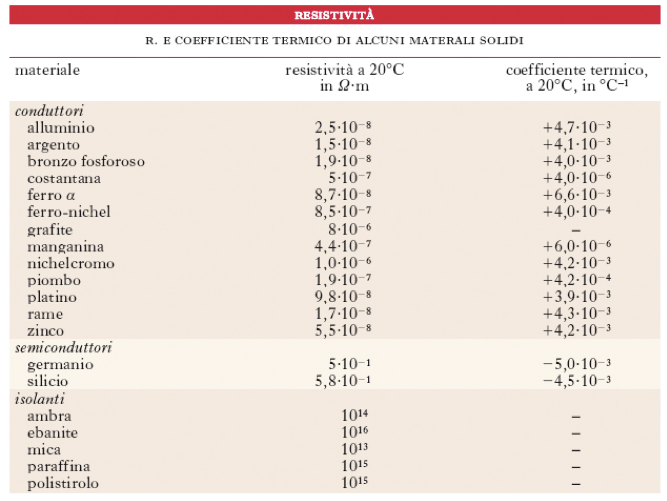
Come si evince dalla tabella sopra, il coefficiente termico α è positivo nei metalli puri come il rame o l'oro mentre esso è negativo nei semiconduttori come germanio e silicio. Ciò vuol dire che in tali materiali all'aumentare della temperatura la resistività decrescerà.
A temperature molto basse alcuni materiali tendono a stabilizzare la resistività verso un valore minimo ρR al di sotto del quale essa non scende.
Invece per altri materiali particolari come il mercurio, al di sotto di una temperatura critica molto bassa (si parla di qualche grado Kelvin) il coefficiente di resistività si annulla rendendo pari a zero dunque la resistenza del materiale. Tali materiali si dicono superconduttori.
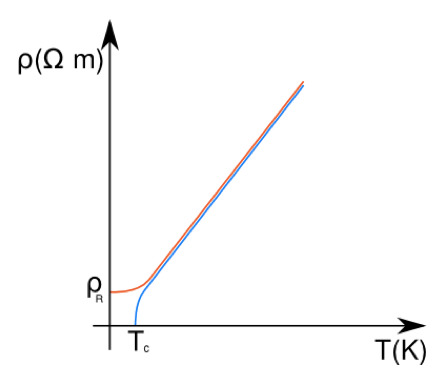
Nel grafico si vede l'andamento del coefficiente di resistività relativo a un materiale che se raffreddato stabilizza il suo coefficiente ρ verso il suo minimo ρR (curva rossa) e l'andamento di ρ per un superconduttore (grafico azzurro).
Link correlati:
Esercizi online e gratuiti sulla seconda legge di Ohm
Come si applica la formula della seconda legge di Ohm
Esercizio sul calcolo della resistenza di un filo di alluminio
Quali sono le formule inverse della seconda legge di Ohm?
Esercizi online e gratuiti sulla prima legge di Ohm
Esercizio svolto sulla termoresistenza
Esercizio sul calcolo della variazione percentuale della resistenza di un conduttore in funzione della temperatura
Studia con noi