Permeabilità magnetica relativa
Che cosa è la permeabilità magnetica relativa?
Iniziamo con il ricordare che la costante di permeabilità magnetica nel vuoto è tra le costanti fondamentali in fisica connessa al calcolo dell'intensità di campo magnetico generato da diverse disposizioni di correnti.
Essa si indica con la lettera greca μ ("mu") e nel vuoto (pedice zero) essa assume questo valore:
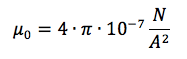
approssimabile col valore numerico di 1,26∙10-6 N/A2.
Permeabilità magnetica relativa
Attraverso la permeabilità magnetica nel vuoto è possibile definire la permeabilità magnetica relativa μr di un materiale e da questa la permeabilità magnetica μ che rappresenta l'attitudine di un corpo a magnetizzarsi se soggetto ad un campo magnetico esterno.
La costante di permeabilità magnetica μ è pari al prodotto della permeabilità magnetica relativa μr , che è una costante tipica di ogni materiale, per la permeabilità magnetica nel vuoto:
μ = μr ∙ μ0
La permeabilità magnetica relativa è un numero puro ovvero una grandezza adimensionale cioè priva di unità di misura. Pertanto la permeabilità magnetica μ ha la stessa unità di misura della permeabilità magnetica nel vuoto, il N/A2.
Proprietà magnetiche dei materiali
Ogni atomo che compone la materia è caratterizzato da un nucleo composto da protoni insieme ai neutroni quindi carico positivo attorno al quale orbitano gli elettroni, che rappresentano le cariche negative.
Questo sistema è schematizzabile come una piccola spira percorsa da corrente in cui sono gli elettroni che orbitano attorno al nucleo a rappresentare la corrente. Ogni spira genera dunque un microcampo magnetico orientato casualmente nello spazio con la determinazione dei due poli Nord e Sud proprio come una vera e propria spira macroscopica, quindi determina un dipolo magnetico.
Ora a seconda di come si orientano questi microscopici dipoli magnetici quando sono soggetti a un campo magnetico esterno possiamo distinguere le sostanze in tre grandi categorie: materiali diamagnetici, paramagnetici e ferromagnetici.
Quando si applica un campo magnetico esterno di intensità B0 ad un certo materiale si ottiene al suo interno un campo magnetico totale di intensità B pari a:
B = μr ∙ B0
cioè pari al prodotto della costante di permeabilità magnetica relativa μr per il modulo del campo esterno applicato.
A seconda del valore che la costante di permeabilità magnetica relativa μr relativa assume si distinguono i materiali diamagnetici, paramagnetici e ferromagnetici rispettivamente se essa risulta di poco inferiore a 1, di poco superiore a 1 o molto superiore a 1.
Permeabilità magnetica nel vuoto e velocità della luce
La relazione tra la costante di permeabilità magnetica nel vuoto e la velocità della luce discende direttamente dalla quarta equazione di Maxwell cioè il teorema di Ampere – Maxwell scritto dal grande fisico scozzese nel 1863 a partire dal precedente teorema sulla circuitazione del campo magnetico di Ampere (teorema di Ampere).
Maxwell ricavò che la velocità c con cui si muoveva un'onda elettromagnetica nello spazio vuoto era legata sia al valore della costante di permeabilità magnetica nel vuoto sia al valore della costante dielettrica nel vuoto dalla relazione:
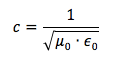
Combinando i due valori delle costanti:
μ0 = 4 ∙ π ∙ 10-7 N/A2
e
ϵ0 = 8,85∙10-12 C2/(N∙m2)
si ottiene un valore di c pari a circa 3∙108 m/s che rappresenta la velocità assunta dalla luce nel vuoto.
Se l'onda si propaga attraverso un mezzo fisico, note le costanti di permeabilità magnetica μ e quella dielettrica ε la velocità dell'onda v si riscrive come:
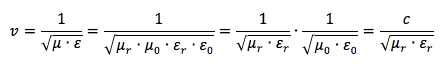
In particolare il prodotto della permeabilità magnetica relativa per la costante dielettrica relativa sotto radice prende il nome di indice di rifrazione n del mezzo e corrisponde al rapporto tra la velocità della luce nel vuoto c e la velocità della stessa onda in un mezzo v:
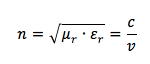
Link correlati:
Esercizi online e gratuiti sul campo magnetico
Esercizio svolto sulla legge di Ampere
Esercizi svolti e commentati di elettrostatica
Studia con noi