Capacità condensatore
Quanto vale la capacità di un condensatore?
Un condensatore è un sistema costituito da due conduttori carichi con la stessa quantità di carica Q ma di segno opposto separati dal vuoto o da un dielettrico.
I due conduttori carichi prendono il nome di armature del condensatore ed essi si caricano sfruttando il fenomeno dell'induzione elettrostatica, modalità di elettrizzazione che non prevede il contatto tra i conduttori.
Tra le due armature si instaura una differenza di potenziale elettrico ΔV visto che il potenziale elettrico dipende dal segno di una carica e le due armature di un condensatore sono caricate l'una positiva e l'altra negativa.
Definizione di capacità di un condensatore
Si definisce capacità del condensatore il rapporto tra il valore assoluto della carica presente su ciascuna armatura Q e la ddp che si instaura tra di esse:
C = Q / ΔV
La carica Q e la ddp tra le armature ΔV sono pari allora a:
Q = C ∙ ΔV
e
ΔV = Q / C
L'unità di misura della capacità elettrica è il farad, simbolo F, che è una unità di misura molto grande e si usano praticamente sempre i suoi sottomultipli in particolare il microfarad, il nanofarad ed il picofarad:
1 μF = 10-6 F
1 nF = 10-9 F
1pF = 10-12 F
La capacità di un condensatore è però indipendente dalla carica ed è determinato esclusivamente dalle caratteristiche geometriche del condensatore.
Vediamo quali sono gli esempi di condensatori con cui si può avere a che fare nei problemi di fisica.
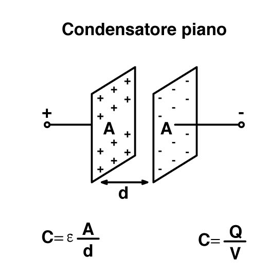
Capacità di un condensatore piano
Un condensatore piano a facce piane e parallele è costituito da due piastre conduttrici separate da un dielettrico o dal vuoto, ognuna di area A e poste tra di loro ad una distanza d.
Dal teorema di Gauss sappiamo che una lastra piana carica genera attorno a se un campo elettrico di intensità pari al rapporto tra la densità superficiale di carica σ e la costante dielettrica nel vuoto ε0 moltiplicata per due:
E = σ / (2 · ε0)
Tale campo sarà uscente per le lastre cariche positive ed entrante per quelle cariche negative.
Se consideriamo adesso un sistema di due lastre con la stessa quantità di carica presente sulle loro superfici ma di segno opposto otteniamo un campo uniforme interno alle due lastre diretto dalla lastra positiva a quella negativa in cui i due campi si sommano ed avrà intensità totale pari a:
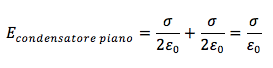
Trattandosi di un campo elettrico uniforme possiamo scriverlo come rapporto tra la differenza di potenziale ΔV tra le armature e la distanza d a cui esse sono poste:
Econdensatore piano = ΔV / d
Per cui uguagliando le due espressioni per il campo elettrico all'interno di un condensatore otteniamo:
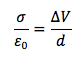
La densità superficiale di carica è il rapporto tra la carica Q presente su ciascuna armatura e la superficie A:
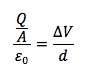
Ricaviamo dalla precedente la capacità di un condensatore piano definita come il rapporto tra carica e ddp:
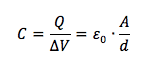
Per cui la capacità di un condensatore piano è direttamente proporzionale alla superficie di ciascuna armatura ed inversamente proporzionale alla distanza a cui esse sono poste.
Se tra le piastre vi è un dielettrico con costante dielettrica relativa εR la capacità si modifica aumentando di un fattore pari proprio ad εR:
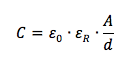
Capacità di un condensatore sferico
Un condensatore sferico è realizzato da un conduttore sferico di raggio R1 al centro di un altro conduttore sferico cavo di raggio interno R2 e raggio esterno R3.
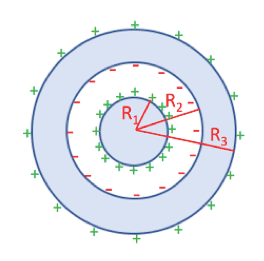
Consideriamo il conduttore interno carico positivamente: sappiamo che la carica si deposita sulla superficie esterna lungo i punti equidistanti R1 dal centro. Per induzione allora sulla superficie interna della sfera cava esterna si manifesterà una carica di segno opposto nei punti distanti R2 dal centro. La capacità di un sistema di questo genere è data da:
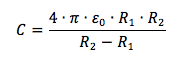
Se tra i due conduttori vi è un dielettrico con costante dielettrica relativa εR la capacità si modifica aumentando di un fattore pari proprio ad εR:
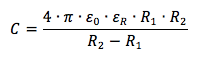
Notiamo che se si fa tendere R2 a +∞, cioè se si isola la sfera conduttrice interna, si torna al caso della capacità di un conduttore sferico isolato. Raccogliendo infatti il termine R2 sia al numeratore sia al denominatore la capacità sarà pari a:
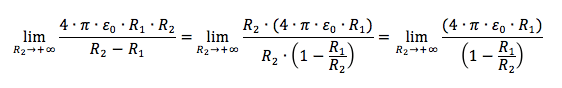
Il rapporto R1/R2 tende a zero visto che R2 tende a +∞, e quindi:
![]()
che rappresenta appunto la capacità di un conduttore sferico isolato.
Capacità di un condensatore cilindrico
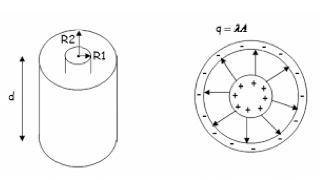
Un condensatore cilindrico è costituito da due superfici cilindriche coassiali di raggio rispettivamente R1 ed R2 ognuna carica con una quantità di carica +Q e -Q.
Si definisce capacità per unità di lunghezza d del condensatore cilindrico:
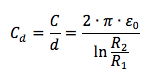
Se tra i due conduttori vi è un dielettrico con costante dielettrica relativa εR la capacità si modifica aumentando di un fattore pari proprio ad εR:
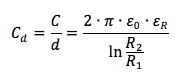
Se si vuole realizzare un condensatore a capacità variabile basta far scorrere le due superfici cilindriche tra di loro in modo da variarne la lunghezza d.
Link correlati:
Esercizio su condensatore piano con armature circolari
Collegamento di due o più condensatori in parallelo
Collegamento di due o più condensatori in serie
Qual è la differenza tra volt e ampere?
Qual è l'unità di misura della capacità elettrica?
Comportamento di diversi circuiti in regime sinusoidale
Studia con noi