Circuiti in corrente alternata
Comportamento di diversi circuiti in regime sinusoidale
In questo sezione del sito analizzeremo sinteticamente il comportamento di diversi circuiti quando sono in regime sinusoidale ovvero quando la tensione e la corrente oscillano secondo una sinusoide.
I circuiti che esamineremo sono:
- il circuito ohmico contenente solo una resistenza R;
- il circuito induttivo contenente solo una induttanza L;
- il circuito capacitivo contenente solo una capacità C;
- il circuito RL (resistenza collegata in serie con una induttanza);
- il circuito RC ( resistenza collegata in serie con un condensatore);
- il circuito LC (induttanza collegata in serie con un condensatore);
- il circuito RLC (resistenza, induttanza e condensatore collegati in serie).
Per ogni circuito in particolare definiremo la misura dell'impedenza Z e la differenza di fase φ tra le oscillazioni della fem e della corrente.
L'impedenza Z di un circuito in particolare si misura in Ω come la resistenza e proprio come quest'ultima rappresenta l'opposizione che un conduttore presenta al passaggio della corrente elettrica alternata.
Circuito ohmico

Z = R
φ = 0
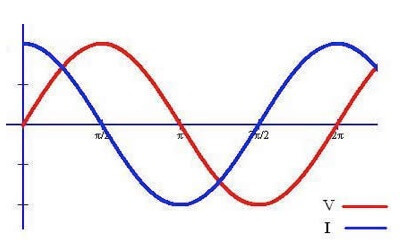
In un circuito ohmico l'impedenza coincide con la resistenza R, la fase tra fem e corrente è zero cioè esse oscillano in fase, cioè quando è massima la tensione è massima la corrente e quando è zero la tensione è zero pure la corrente.
Dette Veff e ieff rispettivamente i valori di tensione e corrente efficaci avremo che:
Z = Veff / ieff = V0 / i0
in cui V0 ed i0 sono i valori di picco della fem e della corrente.
Circuito induttivo
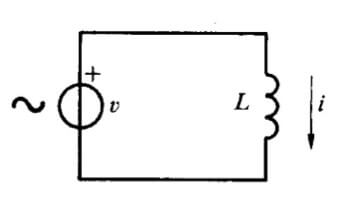
Z = XL = ω ∙ L
φ = - π / 2
In un circuito induttivo l'impedenza si dice reattanza induttiva ed è pari alla pulsazione ω della fem per il valore dell'induttanza L.
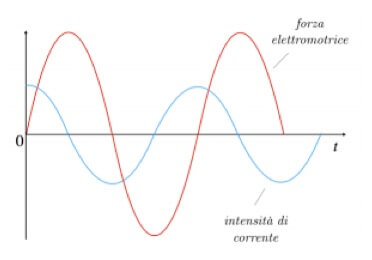
La corrente oscilla in ritardo di un quarto di periodo, cioè π/2 (un periodo completo per le funzioni seno e coseno vale 2π) rispetto alla fem
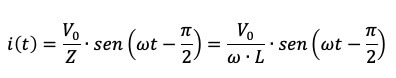
Circuito capacitivo
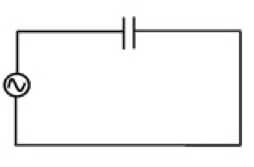
Z = 1 / (ω ∙ C) = Xc
φ = - π / 2
In un circuito capacitivo l'impedenza si dice reattanza capacitiva ed è pari al reciproco del prodotto della pulsazione ω della fem per il valore della capacità C.
La corrente oscilla in anticipo di un quarto di periodo, cioè π/2 (un periodo completo per le funzioni seno e coseno vale 2π) rispetto alla fem:
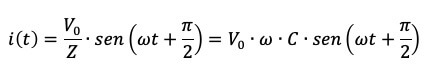
Circuito RL
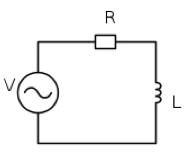
Z2 = R2 + XL2 = R2 + ω2 ∙ L2
φ = arctg (ω ∙ L / R)
Circuito RC
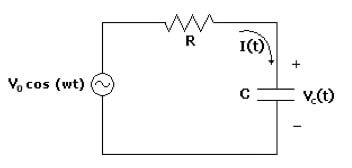
Z2 = R2 + XC2 = R2 + 1 / (ω2 ∙ C2)
φ = arctg [-1 / (ω ∙ C ∙ R)]
Circuito LC
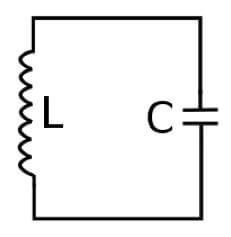
Z = XL - XC = ω ∙ L - 1 / (ω ∙ C)
Per quanto riguarda φ:
φ = 0 se ω = ω0
φ = - π/2 se ω < ω0
φ = π/2 se ω > ω0
in cui:
![]()
Per cui la frequenza di risonanza vale:
![]()
Un circuito LC ha resistenza trascurabile, partendo dalla condizione iniziale in cui il condensatore possiede una quantità di carica iniziale, il circuito produce una corrente oscillante (oscillatore armonico semplice).
Lo sfasamento si avrà tra il periodo di oscillazione della corrente e la presenza delle cariche sulle armature del condensatore.
In particolare la pulsazione ω0 corrisponde alla frequenza di risonanza ovvero le uniche che possono instaurarsi in un circuito LC.
Tali circuiti sono utilizzati per la creazione e la ricezione di onde radio e microonde quindi per la TV, la radio e i telefoni cellulari o il radar.
Utilizzando infatti un condensatore a capacità variabile è possibile variare il valore di C e quindi sintonizzare il circuito alla frequenza desiderata di oscillazione.
Il circuito LC può essere assimilato ad un sistema massa molla in cui non agiscono forze di attrito.
L'oscillazione della massa attraverso la molla rende l'idea del fatto che la corrente continui ad oscillare tra condensatore ed induttore. La corrente oscillerà secondo la relazione:
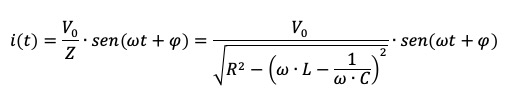
Circuito RLC
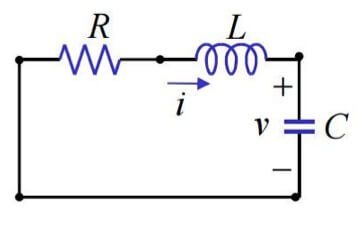

Collegando un circuito RLC ad un'antenna, essa produce oscillazioni all'interno del circuito come se esso fosse collegato ad un generatore di tensione alternata. R rappresenta la resistenza complessiva del circuito.
La corrente oscillerà secondo la relazione:

Il circuito RLC rappresenta il caso reale del circuito LC. Infatti mentre nel circuito LC non è presente alcun elemento che dissipa energia (induttore e capacità hanno resistenza nulla), nel circuito reale RLC l'energia subisce delle perdite essendo presente la resistenza e quindi il sistema rappresenta sempre un oscillatore armonico ma con oscillazioni smorzate fino ad annullarsi.
Questo fenomeno viene eliminato grazie alla presenza di una sorgente di alimentazione esterna.
L'effetto che produce dunque la presenza della resistenza non è altro che uno smorzamento.
In entrambi i circuiti LC e RLC l'intensita' di corrente e' massima quando Z assume il valore minimo Z=R e quindi cio' avviene quando la forza elettromotrice applicata al circuito possiede una pulsazione pari a quella di risonanza.
Infatti per avere Z=R ricordando che
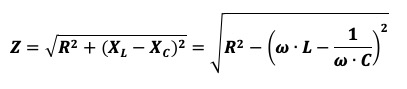
Deve necessariamente risultare:
ω ∙ L = 1 / (ω ∙ C)
Da cui:
![]()
Link correlati:
Esercizio svolto e commentato su circuito induttivo
Esercizio svolto e commentato su circuito RLC
Che cos'è la corrente alternata?
Di quale colore devono essere i fili elettrici?
Che cos'è e quanto vale un microampere?
Che cos'è un tetrodo?
Intensità di corrente elettrica che fluisce in un conduttore in un dato instante
Studia con noi