Esercizi sulla velocità angolare
Esercizi online e gratuiti sulla velocità angolare
In questa sezione del sito sono proposti esercizi sulla velocità angolare.
La raccolta degli esercizi è rivolta sia agli studenti universitari delle facoltà scientifiche che agli studenti di licei ed istituti tecnici.
Prima di procedere allo svolgimento degli esercizi sulla velocità angolare, presentiamo le nozioni di base e le formule fondamentali per affrontare questa categoria di problemi.
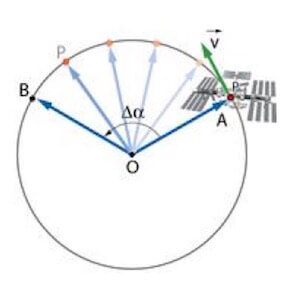
Consideriamo un punto materiale che si muove di moto circolare lungo una circonferenza.
Lungo la sua orbita, il punto materiale percorrerà un arco AB che corrisponde ad un angolo al centro percorso o meglio detto "spazzato"![]() .
.
Detto tale angolo spazzato Δα e Δt il tempo impiegato dal raggio vettore a spazzare l'angolo, si definisce velocità angolare ω il rapporto tra Δα e Δt:
ω = Δα / Δt
L'unità di misura nel Sistema Internazionale è il radiante al secondo [rad/s].
Chimica-online.it inoltre ti offre anche una calcolatrice scientifica.
Esercizi sulla velocità angolare
Di seguito gli esercizi sulla velocità angolare elencati secondo un ordine crescente di difficoltà.
1.
Calcolare velocità tangenziale ed accelerazione centripeta di un elettrone che ruota attorno al nucleo di un atomo di idrogeno, assumendo che l'orbita sia circolare di raggio 5 · 10-11 m e che il periodo sia pari a 1,5 · 10-16 s.
Calcolare infine la velocità angolare.
La soluzione la trovi qui: esercizio sul calcolo della velocità angolare.
2.
Una pattinatrice sta ruotando su se stessa alla velocità angolare di 14 rad/s tenendo le braccia completamente distese.
Ad un certo punto chiude le braccia portandole al proprio petto e facendo diminuire il suo momento di inerzia del 30%.
Calcola la nuova velocità angolare.

Lo svolgimento dell'esercizio lo trovi qui: velocità angolare di un pattinatore.
3.
Lo stadio di nana bianca rappresenta il ciclo finale di una stella di medie dimensioni.
Prima di arrivare in questa forma la stella ruotava con una velocità angolare di 1,1 ∙ 10-6 rad/s.
Sapendo che nel passaggio perde metà della sua massa e che il raggio diventa il 10% di quello iniziale, determinare la nuova velocità angolare.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sulla conservazione del momento angolare.
4.
Un disco di massa 0,2 kg e raggio 20 cm sta ruotando su se stesso quando un oggetto si incastra sul suo bordo per un intervallo di tempo pari a 0,5 s causando il rallentamento della velocità angolare del disco di 5 rad/s.
Determinare la forza media esercitata dal corpo.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sulla accelerazione angolare.
5.
Un'asta di lunghezza 50 cm è inchiodata ad una parete verticale e può ruotare liberamente attorno al suo perno.
Inizialmente l'asta è trattenuta in posizione orizzontale ad un certo stante viene lasciata libera.
Quanto vale l'accelerazione angolare nel momento in cui l'asta forma un angolo di 60° con la verticale?
Lo svolgimento dell'esercizio lo trovi qui: calcolo della velocità angolare.
6.
Un punto materiale si sta muovendo di moto circolare uniformemente accelerato lungo una circonferenza di raggio 2 m.
La sua velocità tangenziale viene misurata all'istante t e vale 1 m/s.
All'istante t + 3s il corpo ha percorso 5 m.
Determinare:
2) la velocità angolare dopo 5 s
3) l'accelerazione centripeta dopo 2 s
4) l'accelerazione tangenziale
5) il numero di giri fatti dopo 10 s
La soluzione la trovi qui: esercizio sul moto circolare uniformemente accelerato.
7.
Un uomo di 80 kg si trova al bordo di una giostra di forma circolare di raggio 3,0 m che sta girando con una velocità angolare di 2,0 rad/s.
Calcola il momento angolare posseduto dall'uomo a causa della rotazione.
Lo svolgimento dell'esercizio lo trovi qui: calcolo del momento angolare.
8.
Un punto materiale si muove lungo una circonferenza il cui raggio misura 15 m con una velocità tangenziale costante pari a 25 m/s.
Calcolare il periodo e la frequenza del moto, l'accelerazione centripeta, e la velocità angolare.
Lo svolgimento dell'esercizio lo trovi qui: calcolo del periodo e della frequenza in un moto circolare uniforme.
9.
Un corpo si muove di moto circolare uniforme lungo una circonferenza lunga 37,68 m, compiendo 1800 giri al minuto.
Calcolare il periodo, la velocità angolare e quale angolo descrive il corpo in 1,5 s.
Lo svolgimento dell'esercizio lo trovi qui: calcolo del periodo in un moto circolare uniforme.
10.
Determina la frequenza e la velocità angolare delle lancette dei secondi, dei minuti e delle ore di un orologio.
Lo svolgimento dell'esercizio lo trovi qui: calcolo della velocità angolare in un moto circolare uniforme.
11.
Le pale di una turbina sono lunghe 6,7 m e ruotano con velocità angolare costante.
Sapendo che la frequenza di rotazione misurata vale 4,5·102 giri /min calcolare la velocità tangenziale degli estremi di una pala e di un punto di una pala posto a 3,5 m dall'asse di rotazione.
Confronta i due valori e commentane i risultati.
Calcola infine il rapporto tra l'accelerazione centripeta della punta della pala con quella del punto che si trova a 3,5 m dall'asse di rotazione.
Lo svolgimento dell'esercizio lo trovi qui: pale di una turbina che ruotano di moto circolare uniforme.
Studia con noi