Radiante
Da gradi a radianti e viceversa
Dato un angolo è possibile misurare questo in due unità di misura o il grado (°) o il radiante (rad).
In particolare un qualsiasi angolo alla circonferenza può essere espresso in radianti facendo il rapporto tra l'arco di circonferenza AB che lo intercetta e il raggio r della circonferenza:
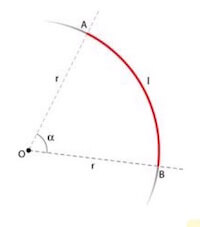
Ovvero:
α = AB / r
Se consideriamo un intero angolo giro (360°) allora l'arco diventerà la lunghezza globale della circonferenza, ovvero 2 · π · r per cui
α360° = 2 · π · r /r = 2 · π
Allora abbiamo dedotto che un angolo di 2 · π radianti vale 360°.
In generale si definisce 1 radiante come l'angolo con vertice al centro della circonferenza tale che l'arco da esso intercettato sia pari alla lunghezza del raggio.
Da gradi a radianti e viceversa
È possibile trasformare i gradi in radianti e viceversa impostando una semplice proporzione.
Abbiamo visto che 2 · π radianti valgono 360° per cui:
αG : αR = 360 : (2 · π)
Da questa proporzione dunque ricaviamo immediatamente l'espressione per ottenere la misura in gradi αG o in radianti αR di un angolo:
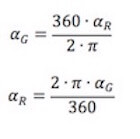
La seguente tabella riporta i principali valori di angoli in gradi coi corrispondenti valori in radianti:
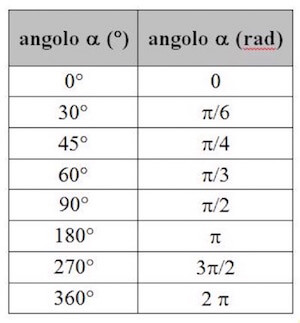
Esercizio in cui bisogna convertire i gradi in radianti
Un punto materiale si sta muovendo di moto circolare uniforme ed ha percorso un angolo di 30° in ⅙ s.
Determinare velocità angolare, periodo del moto e frequenza.
Lo svolgimento dell'esercizio lo trovi qui: calcolo della frequenza in un moto circolare uniforme.
Studia con noi