Esercizio sul moto circolare uniformemente accelerato
Esercizio svolto e commentato sul moto circolare uniformemente accelerato
Un punto materiale si sta muovendo di moto circolare uniformemente accelerato lungo una circonferenza di raggio 2 m.
La sua velocità tangenziale viene misurata all'istante t e vale 1 m/s.
All'istante t + 3s il corpo ha percorso 5 m.
Determinare:
1) l'accelerazione angolare
2) la velocità angolare dopo 5 s
3) l'accelerazione centripeta dopo 2 s
4) l'accelerazione tangenziale
5) il numero di giri fatti dopo 10 s
Svolgimento dell'esercizio
Il corpo ha percorso un arco di circonferenza lungo 5 m.
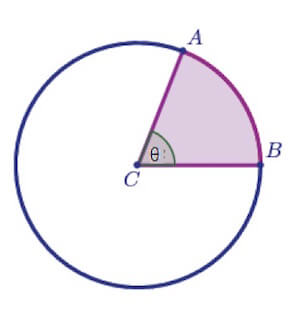
Tale arco corrisponde ad un angolo al centro pari a:
θ = L/r
con L lunghezza dell'arco e r raggio della circonferenza (θ sarà espresso in radianti)
θ = L/r = 5/2 = 2,5 rad
Per applicare la formula:
θ = ½ · α · t2 + ω0 · t + θ0
dobbiamo calcolare la velocità angolare iniziale ω0.
Conosciamo solo la velocità tangenziale iniziale:
V0 = + 1 m/s
Ricordando la relazione che lega V a ω:
V = ω · r
otteniamo
ω = V/r = ½ = 0,5 rad/s
L'accelerazione angolare α allora varrà:
α = 2·[(θ - θ0) - ω0 · t] / t
considerando che
θ - θ0 rappresenta l'angolo spazzato
t è l'intervallo di tempo preso in esame ovvero t + 3 - t = 3 s
allora
α = 2 · [(θ - θ0) - ω0 · t] /t2 = 2 · (2,5 - 0,5 · 3) / 32 = 0,22 rad/s2 (accelerazione angolare)
L'accelerazione angolare è costante.
La legge che lega velocità angolare ed accelerazione angolare è:
ω = ω0 + α · t
per cui all'istante t = 5 s la velocità angolare vale:
ω(5) = 0,5 + 0,22 · 5 = 1,61 rad/s (velocità angolare dopo 5 s)
L'accelerazione centripeta dopo 2 s è data da:
ac = V2/r
in cui V è la velocità tangenziale dopo 2 s.
Calcoliamo dapprima la velocità angolare dopo 2 s e da questa ricaviamo poi la velocità tangenziale che ci occorre per determinare l'accelerazione centripeta.
ω(2) = 0,5 + 0,22 · 2 = 0,94 rad/s
V(2) = ω(2) · r = 0,94 · 2 = 1,89 m/s
Per cui l'accelerazione centripeta dopo 2 s vale:
ac = [V(2)]2 /r = 1,892 / 2 = 1,78 m/s2 (accelerazione centripeta dopo 2 s)
Per il calcolo dell'accelerazione tangenziale invece sfruttiamo la legge oraria relativa al moto rettilineo uniformemente accelerato per cui:
ΔS =½ · a · t2 + V0 · t
da cui
a = 2· [ΔS - V0 · t] / t2 = 2 · (5 - 1 · 3) / 32 = 0,44 m/s2 (accelerazione tangenziale)
Trattandosi di moto circolare uniformemente accelerato l'accelerazione tangenziale è costante, mentre l'accelerazione centripeta varia nel tempo seguendo la variazione della velocità tangenziale.
Dopo 10 s il punto avrà spazzato un angolo (in radianti) pari a:
θ(10) =½ · 0,22 · 102 + 0,5 · 10 + 0 = 16,11 rad
Ora se consideriamo che 2·π rad rappresentano 1 angolo giro (360°) allora possiamo impostare la proporzione:
(2·π) : 360 = 16,11 : x
Ovvero:
x = 16,11· 360/ (2·π) = 923,57°
Poiché; un giro completo è 360°, il punto avrà compiuto:
n = 923,57/360 = 2,56 giri (numero di giri fatti dopo 10 s)
Studia con noi