Esercizi di fluidodinamica
Esercizi online e gratuiti di fluidodinamica
Vengono di seguito proposti alcuni esercizi di fluidodinamica.
La raccolta degli esercizi di fluidodinamica di seguito proposta è rivolta sia agli studenti universitari delle facoltà scientifiche che agli studenti di licei ed istituti tecnici.
Prima di affrontare gli esercizi di fluidodinamica facciamo una brevissima introduzione all'argomento.
Per fluido si intende quel particolare stato della materia che comprende liquidi gas e plasma.
Ogni fluido non ha una forma propria, ma prende la forma del recipiente che lo contiene.
La fluidodinamica è quella parte della meccanica specializzata nello studio del comportamento di un gas o di un liquido quando è posto in movimento.
Dato un recipiente contenente un liquido non viscoso, se viene praticato un foro ad una profondità h, si ha che la velocità di efflusso del liquido dal foro è pari a:
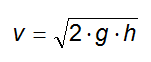
Questa legge è nota come teorema di Torricelli.
Si definisce portata Q di un condotto la quantità di fluido che ne attraversa una sezione in un secondo e si misura in m3/s.
Ipotizzando il fluido come incomprimibile vale l'equazione di continuità, nel caso in cui ci sia una restrizione del condotto il prodotto:
Q = S · v = costante
in cui S è la superficie del condotto attraversata dal fluido e v la velocità.
Quindi la portata si mantiene costante lungo tutto il condotto e S e v risultano inversamente proporzionali tra di loro.
Infine dato un condotto in cui scorre un fluido di densità ρ presi due punti del condotto in cui il fluido scorre con velocità V1 e V2, con pressione P1 e P2 e dette h1 e h2 le quote dei due punti rispetto ad un riferimento orizzontale, vale il teorema di Bernoulli:
P1 + ρ · g · h1 + ½ · ρ · V12 = P2 + ρ · g · h2 + ½ · ρ · V22
Dividendo entrambi i membri per ρ · g otteniamo:
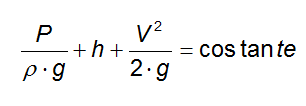
Come conseguenza dell'equazione di continuità e del teorema di Bernoulli, vale il principio di Venturi: se in un condotto la sezione diminuisce, la velocità del fluido che lo attraversa aumenta e la sua pressione diminuisce.
Chimica-online.it inoltre ti mette a disposizione anche una calcolatrice scientifica e un formulario di fisica.
Esercizi sulla fluidodinamica
Di seguito gli esercizi sulla fluidodinamica elencati secondo un ordine crescente di difficoltà.
Livello di difficoltà medio-basso
1.
In un grande serbatoio è contenuta dell'acqua fino ad un'altezza di 8 metri.
Viene praticato un foro 2 metri sotto al livello dell'acqua e ne fuoriesce un getto che arriva a colpire il piano orizzontale ad una certa distanza d dal serbatoio stesso.
calcolare tale distanza.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sulla legge di Torricelli.
2.
Un fluido ideale scorre lungo un condotto.
In un punto P di tale condotto si rileva che il fluido si muove alla velocità di 40 cm/s.
Se la sezione del condotto si restringe passando dai 3 cm2 del punto P ai 2 cm2 di un punto Q, quale sarà la nuova velocità del fluido nella strozzatura?
Lo svolgimento dell'esercizio lo trovi qui: esercizio sull'equazione di continuità.
3.
In un condotto scorrono 7,2 m3 di acqua all'ora alla velocità costante di 1 m/s.
Determinare la sezione del condotto sapendo che essa si mantiene costante lungo tutta la conduttura.
Lo svolgimento dell'esercizio lo trovi qui: calcolo della sezione di un condotto.
4.
In un tubo orizzontale scorre dell'acqua ad una velocità di 4 m/s ed alla pressione di 105 Pa.
Ad un certo punto il tubo si restringe di sezione e la pressione dell'acqua scende a 0,2 ·105 Pa.
Determinare qual è la velocità dell'acqua nella strozzatura e determinare il rapporto tra le due sezioni del tubo.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sull'equazione di Bernoulli.
5.
In un'abitazione è presente una pompa che attraverso un tubo di diametro 3,5 cm porta l'acqua dal piano della strada al primo piano, che si trova ad 8 metri di altezza, ad una velocità di 0,5 m/s e ad una pressione di 206 kPa.
Il tubo passando al primo piano si restringe fino ad un diametro di 1,1 cm.
Lo svolgimento dell'esercizio lo trovi qui: applicazione della legge di Bernoulli.
6.
Un tubo per innaffiare ha un diametro interno di 2 cm e in esso scorre acqua alla velocità di 1 m/s.
Nella parte finale del tubo in cui l'acqua esce fuori, sono presenti 24 fori a sezione circolare ognuno dei quali ha un diametro di 1,2 mm.
Determinare la velocità di fuoriuscita dell'acqua dal tubo.
Lo svolgimento dell'esercizio lo trovi qui: condotto a sezione variabile.
7.
Un serbatoio per l'acqua si trova alla sommità di un edificio ed è riempito tale che il livello superiore arriva a 30 m dal suolo.
Attraverso il serbatoio partono le tubature che portano acqua ai vari appartamenti dell'edificio e tali tubature hanno una sezione molto inferiore alla sezione del serbatoio.
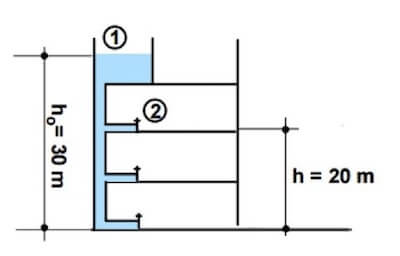
Ogni appartamento è dotato di rubinetteria provvista di orifizi da cui esce l'acqua con sezione di 10 cm2.
Calcolare quanto tempo occorre per riempire un contenitore di capacità 30 dm3 posto in un appartamento che si trova a 20 m dal suolo.
Lo svolgimento dell'esercizio lo trovi qui: velocità di fuoriuscita dell'acqua da un rubinetto.
8.
Il corpo di una siringa di forma cilindrica ha un diametro di 1,2 cm.
Esso contiene un fluido che ha densità doppia rispetto a quella dell'acqua.
Se si esercita una forza di 1 N sullo stantuffo, sapendo che l'ago ha una sezione di diametro 100 µm, calcolare la velocità di fuoriuscita del fluido dall'ago.
Se si pone la siringa in verticale, a che altezza arriverà il getto del fluido?
Lo svolgimento dell'esercizio lo trovi qui: esercizio sulla legge di Bernoulli.
Livello di difficoltà medio-alto
9.
Si ha la necessità di far fuoriuscire un fluido posto all'interno di una siringa senza ago, posta in orizzontale, alla velocità di 15 cm/s.
Stabilire quale differenza di pressione ci deve essere tra lo stantuffo e il beccuccio da cui fuoriesce il fluido, se il rapporto tra le due sezioni vale 20 e il fluido contenuto all'interno della siringa ha densità pari a quella dell'acqua.
Lo svolgimento dell'esercizio lo trovi qui: teorema di Bernoulli applicato ad un condotto orizzontale.
10.
Un grande recipiente cilindrico alto 10 m ed aperto superiormente contiene dell'acqua.
Alla base del silos è presente una piccola conduttura orizzontale da cui l'acqua può fuoriuscire.
Calcolare quale deve essere la sezione del tubo affinché l'acqua in uscita possa avere una potenza di almeno 10 kW.
Considerare la pressione atmosferica pari a 1 atm.
Lo svolgimento dell'esercizio lo trovi qui: esercizio con teorema di Torricelli e legge di Stevino.
11.
Una conduttura in cui scorre dell'acqua è posta in modo tale che la seconda estremità è posta 50 cm più in alto rispetto alla prima, ed è aperta e a contatto con l'atmosfera.
La portata con cui scorre il fluido all'interno è pari a 5 litri / minuto.
La sezione del tubo al primo estremo vale 2 cm2, mentre la sezione al secondo estremo, quello rialzato, vale 0,5 cm2.
Calcolare:
1) quanta acqua fluisce nel tubo in 3 secondi;
2) la velocità dell'acqua ai due estremi;
3) quanto vale la pressione all'estremo di entrata.
Lo svolgimento dell'esercizio lo trovi qui: Bernoulli e conduttura inclinata in cui scorre dell'acqua.
12.
Un venturimetro (tubo di Venturi) o è un dispositivo costituito da un tubo orizzontale in cui è presente una strozzatura centrale che serve a calcolare la velocità con cui scorre un fluido al suo interno:
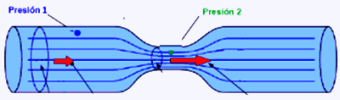
Nei due punti indicati in figura, ovvero prima della strozzatura e lungo la strozzatura, sono posizionati due manometri che misurano la pressione del fluido.
Calcolare in funzione della differenza di pressione, della densità del fluido e delle caratteristiche fisiche del condotto, la velocità con cui scorre il fluido.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sul venturimetro.
13.
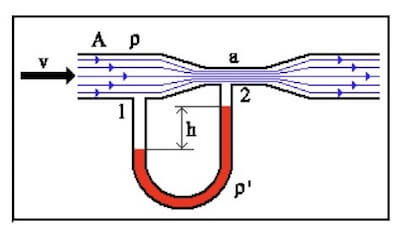
Un venturimetro è realizzato attraverso l'utilizzo di un tubo manometrico, ovvero un tubo a U le cui due estremità sono connesse a un condotto orizzontale che presenta una strozzatura.
Una delle due estremità è posta in corrispondenza dell'inizio del condotto mentre la seconda è posta nella strozzatura.
Sapendo che il fluido ha densità ρ, che le due sezioni sono A ed a, che dentro al tubo manometrico è presente del mercurio di densità ρ' e che si rileva una differenza di altezza h tra i due rami del tubo a U, determinare la velocità V del fluido all'inizio del condotto.
Lo svolgimento dell'esercizio lo trovi qui: velocità di un fluido all'inizio di un condotto.
Livello di difficoltà alto
14.
Per riempire una piscina si utilizzano due diverse pompe che hanno una diversa portata.
La seconda pompa impiegherebbe 2 ore di tempo in più rispetto alla prima se dovesse riempire da sola la piscina.
Mentre se usate contemporaneamente le due pompe impiegano un tempo totale di 1 ora e 20 minuti.
Quanto tempo impiegherebbero le due pompe se dovessero separatamente riempire la piscina?
Lo svolgimento dell'esercizio lo trovi qui: pompe con portata diversa.
15.
Dimostrare a partire dal teorema di Bernoulli che dato un recipiente contenente un liquido non viscoso, se viene praticato un foro ad una profondità h dal livello superficiale del liquido, si ha che la velocità di efflusso del liquido dal foro è pari a:

(legge di Torricelli)
Si esamini successivamente il caso di un piccolo recipiente d'acqua di forma cilindrica che abbia diametro pari a 0,10 m e di altezza pari a 0,20 m.
Viene praticato un foro dalla superficie di 1 cm2 lateralmente ed in corrispondenza della base.
L'acqua fuoriesce da tale foro con una portata di 1,4 · 10-4 m3/s.
Determinare l'altezza del livello dell'acqua contenuta nel recipiente ed il tempo impiegato per svuotarsi completamente.
Lo svolgimento dell'esercizio lo trovi qui: Bernoulli e velocità di fuoriuscita di un liquido.
Altri esercizi li trovi qui:
Esercizio sul calcolo della prevalenza di una pompa
Studia con noi