Quantità di moto relativistica
Che cos'è la quantità di moto relativistica?
Si definisce quantità di moto relativistica il prodotto tra la massa relativistica m di un corpo e il vettore velocità v:
P = m · v
NB = in grassetto vengono indicate le grandezze vettoriali.
Ricordando che l'espressione della massa relativistica in funzione della massa a riposo m0 è:
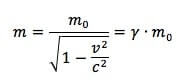
Per cui:
P = γ · m0 · v
Allora il modulo della quantità di moto si può scrivere come:
in cui v è la velocità del sistema di riferimento inerziale S' che si sta muovendo rispetto ad un altro sistema di riferimento S.
A differenza del caso classico in cui la quantità di moto rimaneva direttamente proporzionale alla velocità, adesso nel caso relativistico la dipendenza non è più lineare comparendo v anche nel fattore relativistico.
Bisogna utilizzare la quantità di moto relativistica ogniqualvolta le velocità prese in esame risultano considerevoli rispetto a quella della luce.
Conservazione della quantità di moto relativistica
Così come nel caso classico, anche quando si trattano velocità prossime a quella della luce, vale il principio di conservazione della quantità di moto.
La quantità di moto relativistica iniziale sarà uguale alla quantità di moto relativistica finale di un sistema se la risultante delle forze su di esso agenti è nulla.
Pi = Pf
Se sono presenti più corpi bisognerà imporre che la somma vettoriale di tutte le quantità di moto iniziali riferite ai singoli corpi sia pari alla somma delle quantità di moto finali degli stessi.
Trattandosi infine di vettori, se essi sono composti da più componenti, ovvero le velocità hanno delle componenti x e y, bisognerà imporre la conservazione di P sia sull'asse x sia sull'asse y.
L'invariante energia – quantità di moto
Partiamo dall'espressione della massa relativistica espressa come:
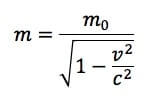
Elevando al quadrato ambo i membri, sviluppando il m.c.m. e rielaborando l'equazione, si ha che:
m2 ∙ (c2 - v2) = m02 ∙ c2
m2 ∙ c2 - m2 ∙ v2 = m02 ∙ c2
Ricordando che E= m∙c2 e che quindi risulterebbe:
E2 = m2 ∙ c4
possiamo moltiplicare tutti i termini dell'equazione sopra per c2, ottenendo:
m2 ∙ c4 - m2 ∙ v2 ∙ c2 = m02 ∙ c4
Per cui poiché p = m∙v otteniamo:
E2 - p2 ∙ c2 = m02 ∙ c4
Quindi se un corpo è in quiete rispetto a un certo sistema di riferimento (v=0) allora avrà quantità di moto nulla. In questo caso la sua energia sarà uguale all'energia a riposo:
E = m0 ∙ c2
Se invece il corpo si sta muovendo a una certa velocità rispetto ad un dato sistema di riferimento allora si evince che la quantità E2 - p2 ∙ c2 deve essere pari a una costante ovvero m02 ∙ c4 cioè il prodotto tra il quadrato della massa a riposo (invariante) e la velocità della luce elevata alla quarta potenza (invariante).
Quindi non dipende più dal sistema di riferimento e tale differenza risulta invariante rispetto alle trasformazioni di Lorentz. Tale grandezza viene detta invariante energia quantità moto.
In particolare la quaterna ordinata E/c, px, py, pz rappresentano le 4 componenti del quadrivettore energia - quantità di moto e durante l'evoluzione di un sistema è proprio il modulo di questo quadrivettore che si conserva e non cambia.
La quantità di moto della luce
Einstein nel 1905 ipotizzò che la luce fosse composta da corpuscoli detti fotoni, privi di massa e viaggianti proprio alla velocità della luce c. Essendo dunque per i fotoni m0 = 0, si ottiene allora
E2 - p2 ∙ c2 = 0
Da cui
p = E / c
Dunque la quantità di moto associata alla luce è pari al rapporto tra l'energia trasportata dall'onda e la velocità della luce. Quando la luce interagisce con la materia, può trasferire parte di questa energia alle particelle fisiche e considerando il sistema fotone + particella come un sistema isolato, si può affermare che la quantità di moto del sistema si conserva, come se si scontrassero due palline di biliardo (effetto Compton).
L'energia cinetica
Dato un corpo con massa a riposo m0 che si muove a velocità v nel sistema di riferimento inerziale assegnato, esso possiede un'energia pari all'energia a riposo (m0 ∙ c2) più il termine relativo alla velocità ovvero l'energia cinetica relativistica.
Questo termine cinetico sarà pari alla differenza tra l'energia totale e l'energia a riposo ovvero in formule:
EK = (γ-1)∙ m0 ∙ c2
con γ fattore relativistico.
Link correlati:
Esercizio sul calcolo della quantità di moto relativistica totale di un sistema
Cosa rappresenta l'equazione E = m ∙ c2?
Esercizio sul calcolo del fattore di Lorentz
Esercizio sul calcolo del fattore relativistico
Esercizi online e gratuiti sulla quantità di moto
Studia con noi