Risoluzione di un circuito e calcolo della potenza dissipata su ciascuna resistenza
Risoluzione di un circuito elettrico e calcolo della potenza dissipata su ciascuna resistenza
Risolvere il circuito in figura sapendo che:
V = 12 V
R1 = R3 = R4 = R6 = 2 Ω
R2 = R5 = R7 = R8 = 4 Ω
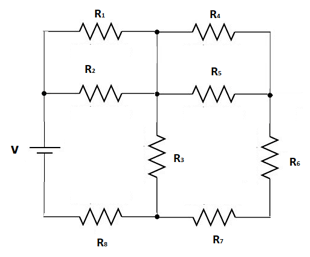
Calcolare inoltre la potenza dissipata su ciascuna resistenza.
Svolgimento dell'esercizio
Per risolvere il circuito e determinare tutte le tensioni e le correnti presenti in esso, attribuiamo convenzionalmente il verso a tensioni e correnti nei vari rami.
Partiamo dalle correnti: nel ramo in cui è presente l'unico generatore di tensione, il verso convenzionale della corrente è quello che esce dal polo positivo e va verso il polo negativo.
Inoltre segniamo il verso delle tensioni ai capi di generatori e resistenze con le regole che conosciamo.
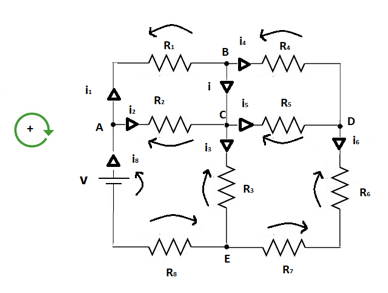
Identifichiamo in tutto 8 diverse correnti e quindi 8 diverse incognite. Abbiamo dunque bisogno di 8 differenti equazioni non combinate linearmente tra di loro ma indipendenti in modo da poter risolvere il sistema di 8 equazioni in 8 incognite.
Scriviamo le leggi dei nodi a tutti i nodi presenti nel circuito:
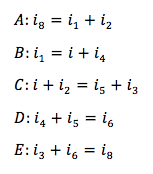
Queste appena scritte rappresentano 5 delle 8 equazioni di cui abbiamo bisogno.
Ricaviamo altre 4 equazioni attraverso le leggi delle maglie.
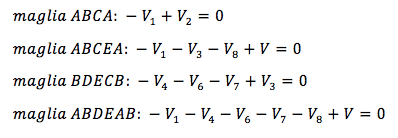
Applichiamo la prima legge di Ohm e scriviamo le tensioni ai capi delle resistenze come prodotto della resistenza per la corrente che la attraversa:
V1 = R1 ∙ i1
V2 = R2 ∙ i2
V3 = R3 ∙ i3
V4 = R4 ∙ i4
V5 = R5 ∙ i5
V6 = R6 ∙ i6
V7 = R7 ∙ i6
V8 = R8 ∙ i8
Sostituendo alle quattro equazioni precedenti si ha che:
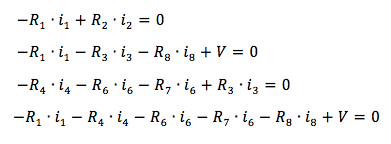
Il sistema da risolvere comprensivo delle otto equazioni è quindi:
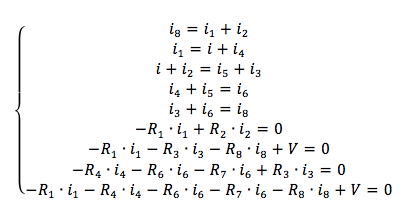
Sostituiamo i valori numerici:
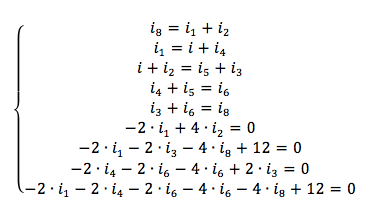
Otteniamo i seguenti risultati:
i = -6/11 A
i1 = 12/11 A
i2 = 6/11 A
i3 = 18/11 A
i4 = 18/11 A
i5 = -18/11 A
i6 = 0
i8 = 18/11 A
Rispetto ai versi delle correnti indicati le correnti i ed i5 hanno un verso effettivo opposto.
Le tensioni ai capi di ciascuna resistenza valgono:
V1 = R1 ∙ i1 = 2∙12/11 = 24/11 V
V2 = R2 ∙ i2 = 4∙6/11 = 24/11 V
V3 = R3 ∙ i3 = 2∙18/11 = 36/11 V
V4 = R4 ∙ i4 = 2∙18/11 = 36/11 V
V5 = R5 ∙ i5 = 4∙18/11 = 72/11 V
V6 = R6 ∙ i6 = 2∙0 = 0 V
V7 = R7 ∙ i6 = 4∙0 = 0 V
V8 = R8 ∙ i8 = 4∙18/11 = 72/11 V
Le potenze dissipate su ciascuna resistenza sono pari a:
P1 = R1 ∙ i12 = 2∙(12/11)2 = 2,38 W
P2 = R2 ∙ i22 = 4∙(6/11)2 = 1,19 W
P3 = R3 ∙ i32 = 2∙(18/11)2 = 5,36 W
P4 = R4 ∙ i42 = 2∙(18/11)2 = 5,36 W
P5 = R5 ∙ i52 = 4∙(18/11)2 = 10,71 W
P6 = R6 ∙ i62 = 2∙0 = 0 W
P7 = R7 ∙ i62= 4∙0 = 0 W
P8 = R8 ∙ i82 = 4∙(18/11)2 = 10,71 W
Link correlati:
Esercizio svolto sulle leggi di Kirchhoff
Esercizio su resistori in serie
Collegamento di resistenze in serie
Come avviene la trasformazione stella triangolo?
Esercizio svolto sulla trasformazione stella triangolo
Qual è l'unità di misura della resistività?
Studia con noi