Esercizio sulle leggi di Kirchhoff
Esercizio svolto sulle leggi di Kirchhoff
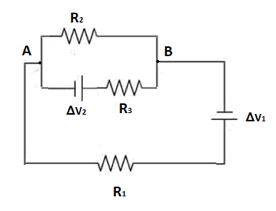
Nel circuito in figura si conoscono i valori di : ΔV1 = 9 V, ΔV2 = 6 V, R1 = 1 Ω, R2 = 3 Ω, R3 = 1Ω.
Determina in verso e valore tutte le correnti presenti nel circuito.
Svolgimento dell'esercizio
Per risolvere il circuito e determinare tutte le correnti presenti in esso, attribuiamo convenzionalmente il verso a tensioni e correnti nei vari rami.
Partiamo dalle correnti: nei rami in cui sono presenti i generatori di tensione, il verso convenzionale della corrente è quello che esce dal polo positivo e va verso il polo negativo.
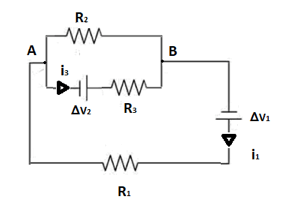
Nel nodo A quindi entra la corrente i1 ed esce la corrente i3. Ipotizziamo che esca anche la corrente i2 dallo stesso nodo.
Inoltre segniamo il verso delle tensioni ai capi di generatori e resistenze con le note regole.
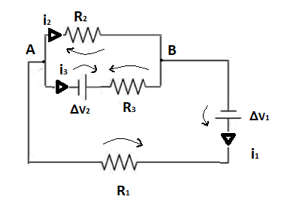
Scriviamo la legge dei nodi e la legge delle maglie per il circuito. Scegliamo come positivo il verso orario ed individuiamo le maglie presenti nel circuito:
maglia 1 : R2 – R3 – ΔV2 – R2
maglia 2 : R2 – ΔV1 – R1 – R2
maglia 3: ΔV2 – R3 - ΔV1 – R1 - ΔV2
Per il nodo A vale la relazione:
i1 = i2 + i3
Per il nodo B:
i2 + i3 = i1
le due equazioni sono equivalenti.
Dobbiamo cercare altre due relazioni essendo 3 le incognite (i1, i2 e i3).
Scriviamo la legge delle maglie per la maglia 1.
Indichiamo con V1, V2 e V3 le tensioni ai capi rispettivamente di R1, R2 ed R3:
-V2 + V3 – ΔV2 = 0
Mentre per la maglia 2:
-V2 + ΔV1 – V1 = 0
Applichiamo la prima legge di Ohm e scriviamo le tensioni ai capi delle resistenze come prodotto della resistenza per la corrente che la attraversa:
V1 = R1 ∙ i1
V2 = R2 ∙ i2
V3 = R3 ∙ i3
Allora le due leggi delle maglie scritte sopra diventano:
- R2 ∙ i2 + R3 ∙ i3 – ΔV2 = 0
- R2 ∙ i2 + ΔV1 – R1 ∙ i1 = 0
Il sistema da risolvere comprensivo delle tre equazioni è quindi:
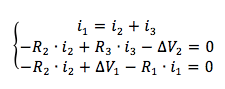
Sostituiamo i valori numerici:
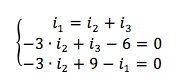
Risolvendo il sistema per sostituzione progressiva si ha che:
i1 = 54/7 A
i2 = 3/7 A
i3 = 51/7 A
I versi delle correnti indicati nel disegno sono dunque tutti corretti in quanto i risultati sono tutti di segno positivo.
Link correlati:
Esercizio su resistori in serie
Collegamento di resistenze in serie
Che cosa afferma il teorema di Tellegen?
Qual è l'unità di misura della resistività?
Esercizio svolto sul principio di sovrapposizione degli effetti
Risoluzione di un circuito elettrico e calcolo della potenza dissipata su ciascuna resistenza
Studia con noi