Esercizio sul principio di sovrapposizione degli effetti
Esercizio svolto sul principio di sovrapposizione degli effetti
Nel circuito in figura:
E1 = 100 V
E2 = 150 V
R1 = 10 Ω
R2 = 20 Ω
R3 = 5 Ω
R4 = 35 Ω
IG = 4A
Determinare la corrente che scorre nella resistenza 1 e 3. Considerare i generatori ideali.
Svolgimento dell'esercizio
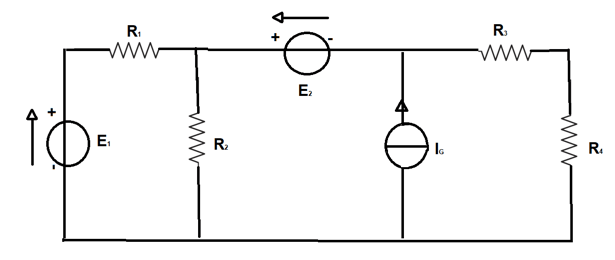
Il circuito in figura è costituito da tre generatori ideali: due di tensione ed uno di corrente. Sono inoltre presenti quattro resistenze e le incognite sono le correnti che scorrono nella resistenza 1 e 3 rispettivamente IR1 e IR3.
Risolviamo il problema applicando il principio di sovrapposizione degli effetti essendo il circuito costituto da resistenze e generatori ideale avrà caratteristica lineare.
Iniziamo col considerare soltanto il generatore E1 ed annulliamo gli altri due sostituendo rispettivamente al generatore ideale di tensione il cortocircuito e al generatore ideale di corrente il circuito aperto:
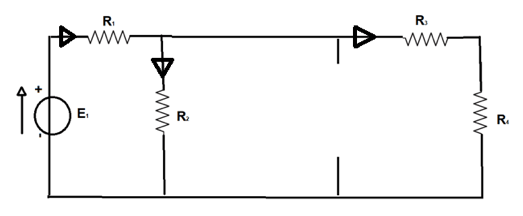
In questa configurazione la serie di R3 e R4 è in parallelo con R2. Il loro parallelo è in serie con R1. Quindi per trovare la resistenza equivalente del circuito calcoliamo la serie tra la terza e la quarta resistenza come somma
R34 = R3 + R4 = 5 Ω + 35 Ω = 40 Ω
Adesso calcoliamo la resistenza equivalente del parallelo tra quest'ultima e R2:
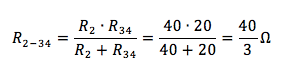
Infine la resistenza equivalente del circuito è la somma di R1 con quest'ultima:
Req = 10 Ω + 40/3 Ω = 70/3 Ω
La corrente che circola nella resistenza equivalente è pari a:
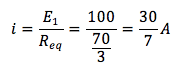
Tale corrente è anche quella che scorre in R1 e rappresenta il primo risultato parziale per determinare la corrente totale che scorre attraverso questa resistenza. La tensione sull'equivalente di R2 con R34 è:
V2-34 = R2-34 ∙ i = 40/3 ∙30/7 = 400/7 V
La corrente che scorre nella serie tra R3 ed R4 è
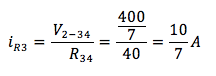
Allora considerando solo E1 otteniamo: iR1 = 30/7 A e iR3 = 10/7 A entrambe verso destra.
Passiamo adesso a considerare solo E2. Otteniamo questa configurazione circuitale:
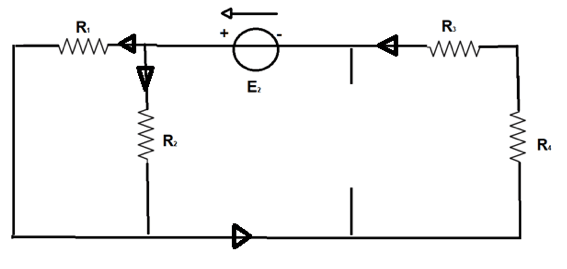
Le resistenze R1 ed R2 sono in parallelo ed il loro sistema risulta in serie con R3 e R4.
Calcoliamo la resistenza equivalente del parallelo tra R1 ed R2:

La resistenza equivalente totale è la somma di quest'ultima con R3 e R4:
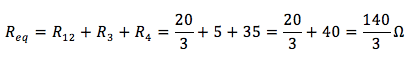
La corrente che scorre nel circuito è
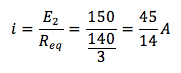
Questa sarà la corrente che scorre in R3 e determina una tensione del parallelo tra R1 ed R2 di
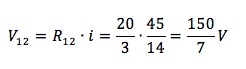
La corrente su R1 è allora:
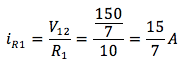
Allora considerando solo E2 otteniamo: iR1 = 15/7 A e iR3 = 45/14 A entrambe verso sinistra.
Infine consideriamo solo il generatore ideale di corrente IG:
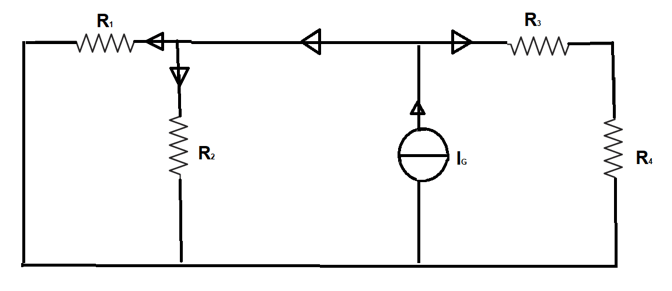
Le resistenze R1 ed R2 sono in parallelo ed il loro sistema risulta in parallelo con R3 e R4. Calcoliamo la resistenza equivalente del parallelo tra R1 ed R2:
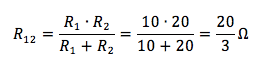
La resistenza equivalente totale è il parallelo di quest'ultima con la serie di R3 e R4:
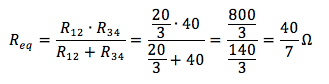
La tensione su questa resistenza vale
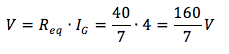
La corrente allora su R1 è
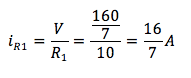
La corrente su R3:
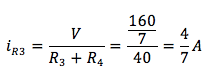
Allora considerando solo IG otteniamo: iR1 = 16/7 A e iR3 = 4/7 A la prima verso sinistra e la seconda verso destra.
Per il principio di sovrapposizione degli effetti sommiamo adesso le tre correnti ottenute per ciascuna resistenza rispettando i segni (positivo verso destra, negativo verso sinistra):

I risultati delle correnti definitive sono orientate entrambe verso sinistra mentre in valore assoluto valgono:
iR1 = 0,14 A
iR3 = 1,21 A
Link correlati:
Collegamento di resistenze in parallelo
Collegamento di resistenze in serie
Studia con noi