Relatività generale
Postulati su cui si fonda la relatività generale
Esistono due diversi modi di definire la massa che portano al concetto di massa inerziale e massa gravitazionale.
La massa inerziale minerziale è quella che discende dal secondo principio della dinamica ed è definita come il rapporto tra la forza applicata ad un corpo e l'accelerazione impressa:
minerziale = F / a
La massa gravitazionale mg è invece quella che compare nella formula della gravitazione universale di Newton:
F = G · Mterra · mg / d2
che esprime la forza di attrazione gravitazionale tra la Terra di massa Mterra (si veda: massa Terra) ed un qualsiasi corpo di massa (gravitazionale appunto) mg.
Il campione unitario della massa gravitazionale è il chilogrammo, rappresentato dal cilindro di platino iridio conservato a Sevres.
Ora si dimostra sperimentalmente che le due masse considerate sono in realtà la stessa cosa e coincidono.
Infatti il secondo principio della dinamica permette di calcolare la forza peso a cui sono soggetti i corpi sulla Terra come:
F = minerziale ∙ g
In cui g è il valore dell'accelerazione di gravità 9,8 m/s2 con cui tutti i corpi cadono verso il suolo.
Sostituendo tale espressione nella formula della forza gravitazione otteniamo:
minerziale ∙ g = G · Mterra · mg / d2
Da cui possiamo ricavare il valore dell'accelerazione di gravità g come:
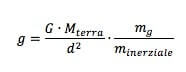
Sperimentalmente si osserva che il rapporto tra la massa gravitazionale e la massa inerziale che compare nella precedente equazione è uguale a 1 poiché l'accelerazione di gravità g è indipendente dalla massa dei corpi.
Concludiamo allora che massa gravitazionale e massa inerziale devono necessariamente essere proporzionali tra di loro ed il loro rapporto deve valere 1 visto che in una data regione dello spazio l'accelerazione di gravità g è uguale per tutti i corpi indipendentemente dalla loro massa.
Caduta libera ed assenza di peso
Il famoso esperimento ideale dell'ascensore in caduta libera proposto da Einstein aveva come scopo quello di provare che può esistere un sistema di riferimento in una certa regione dello spazio tempo in cui simulare l'eliminazione degli effetti della forza di gravità.
Se infatti immaginiamo un corpo presente all'interno di un ascensore in caduta libera vedremmo che esso avvertirebbe l'assenza totale di peso e galleggerebbe all'interno del sistema di riferimento non inerziale ascensore.
Lo stesso principio che vale sulla stazione orbitante attorno alla Terra. In realtà la stazione è in costante caduta libera verso la Terra e contemporaneamente in un'orbita circolare attorno al pianeta.
Tale caduta libera consente agli astronauti presenti al suo interno, anche in questo caso un sistema di riferimento non inerziale, l'assenza di gravità e dunque il galleggiamento.
Analogo caso è quello degli aerei a gravità zero che fanno provare ai propri passeggeri per qualche secondo il volo "a zero g".
In tutti questi casi chiunque si trovi all'interno di uno di questi esempi di sistemi di riferimento non inerziali in cui non si rileva più la forza gravitazione ma l'assenza di peso, non potrebbe compiere alcun esperimento che gli consenta di capire in quale sistema di riferimento preciso si trovi, cioè se ad esempio nell'ascensore ideale di Einstein in caduta libera o nella stazione spaziale.
Accelerazione del sistema e forza peso
Immaginiamo adesso che un corpo si trovi dentro a un'astronave nello spazio profondo molto lontano da qualsiasi corpo celeste massivo tale da non risentire di alcun effetto gravitazionale.
Se ad un certo punto l'astronave inizia ad accelerare allora il corpo che fino a quando l'astronave era ferma poteva galleggiare nel sistema, adesso invece risente di una forza peso fittizio proprio come se ci fosse una massa di un pianeta ad attirarlo.
Potremmo anche pensare all'ascensore che anziché cadere in caduta libera sulla terra stavolta sta accelerando verso l'alto. In tale caso si sperimenta un'accelerazione di gravità superiore a g e quindi è come se si creasse un altro campo gravitazionale che si va a sommare a quello terrestre.
Anche in questo caso come nel caso complementare della simulazione dell'assenza di campo gravitazionale in caduta libera, chiunque si trovi all'interno di uno di questi esempi di sistemi di riferimento non inerziali in cui si rileva l'esistenza di un campo gravitazionale uniforme anziché l'assenza di peso o la normale accelerazione di gravità g, non potrebbe compiere alcun esperimento che gli consenta di capire in quale sistema di riferimento preciso si trovi, cioè se ad esempio nell'astronave in accelerazione o nell'ascensore ideale di Einstein in accelerazione costante verso l'alto.
Link correlati:
Che cos'è la massa relativistica?
Esercizio sul calcolo dell'energia liberata durante il processo di decadimento radioattivo
Esercizio sulla frequenza cardiaca perpecita da un astronauta e relatività ristretta
Esercizio svolto e commentato sulla simultaneità di due eventi
Cosa rappresenta l'equazione E = m ∙ c2?
Esercizio sul calcolo del fattore di Lorentz
Esercizio sul calcolo del fattore relativistico
Che cosa sono e come si formano i buchi neri?
Che cos'è l'equazione di campo di Einstein?
Che cosa sono le onde gravitazionali?
Studia con noi