Equazione di campo di Einstein
Che cos'è l'equazione di campo di Einstein?
Come è noto le masse deformano la struttura spazio temporale dell'universale che risulta come curva.
Qualunque corpo di massa più piccola, compresa la luce, che si trovi in prossimità di tali masse è costretto a muoversi lungo percorsi quindi che non sono rettilinei bensì curvi, seguendo la geometria dello spazio tempo curvo, e ciò porta a conseguenze sconcertanti come nella dilatazione gravitazionale dei tempi.
L'equazione di campo di Einstein consente di calcolare quale sia la geometria dello spazio una volta che risulta nota la distribuzione delle masse.
Curve geodetiche
Una curva geodetica o geodetica rappresenta la minima distanza che unisce due punti nello spazio tempo.
In uno spazio euclideo piatto le curve geodetiche sono delle rette, in uno spazio curvo ad esempio quella su di una superficie sferica sono invece archi di circonferenza.

Le cose si fanno molto più complicate quando passiamo dalla rappresentazione dello spazio tempo a una dimensione spaziale ed una temporale (diagramma di Minkoswky) a una a tre dimensioni in cui pensiamo di curvare tale diagramma.
In un diagramma di Minkowsky infatti un punto era rappresentato da una retta la cosidetta linea d'universo che forniva la coordinata spaziale e temporale contemporaneamente (cioè il dove e il quando di un evento).
La serie di tutti i punti di una retta forniva dunque la rappresentazione di un fenomeno e l'inclinazione della retta era direttamente collegata con la velocità.
Adesso in una rappresentazione a 3 dimensioni le rette diventano superfici curve e pertanto in tale spazio non vale più la geometria euclidea.
Le geometrie non euclidee
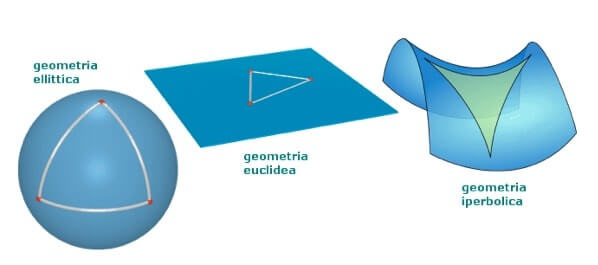
Le più importanti geometrie non euclidee da ricordare sono quelle ellittiche ed iperboliche.
Nelle geometrie ellittiche non è possibile avere rette parallele ad una data retta, che passino per un punto esterno ad essa ed inoltre la somma degli angoli interni di un triangolo tracciato su di una tale superficie ellittica è tale per cui la somma degli angoli interni è sempre maggiore di 180°.
Nelle geometrie iperboliche invece è possibile individuare infinite rette parallele ad una data retta che passino per un punto esterno a quest'ultima.
In questo caso la somma degli angoli interni di un triangolo tracciato su di una tale superficie iperbolica è sempre minore di 180°.
L'equazione di campo
Quando si ha a che fare con sistemi di riferimento non inerziali, cioè accelerati, si possono approssimare come inerziali solo alcune zone locali dell'intero sistema e solo per brevi istanti di tempo.
Ciò vorrebbe dire approssimare un grande spazio curvo con uno piatto limitatamente ad una piccola porzione di esso, come per esempio la Terra che ha una grandissima superficie curva ma che a noi, solo localmente, appare come piatta.
In un universo approssimato come piatto le leggi di Newton risultano ancora valide.
Matematicamente Einstein descrive questo spazio tempo con un'equazione che lega la curvatura Gμν di un punto dello spazio tempo al tensore Tμν (cioè una generalizzazione del concetto di vettore) energia cioè che la curvatura dello spazio è direttamente proporzionale alla densità di energia.
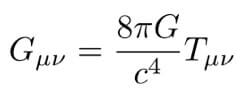
Il significato fisico di questa equazione è che lo spazio tempo curvo è il risultato di una certa densità di energia e quindi materia ricordando che E = m ∙ c2 e più esso è incurvato più alta sarà allora l'attrazione gravitazionale.
In realtà quella sopra scritta è una semplificazione dell'equazione a cui giunse Einstein che invece presenta una forma specifica della curvatura dello spazio tempo ed è la seguente:
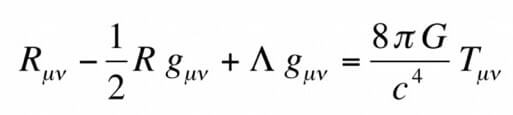
La soluzione di questa equazione esulta dai programmi delle scuole superiori a livello nazionale e viene trattato solo in ambito universitario per la complessità matematica che la sostiene.
Tuttavia è interessante discutere che si perviene ad un risultato circa la geometria dell'universo che viene definita in rapporto alla velocità di espansione dell'universo stesso e alla densità di energia/materia.
In sostanza la densità di energia/massa influenza la velocità di espansione dell'universo ed esiste una soglia critica di densità al di sotto della quale si ha un universo aperto che continuerà ad espandersi per sempre mentre al di sopra si avrà un universo chiuso che è destinato inesorabilmente a contrarsi.
Link correlati:
Che cosa afferma e su quali postulati si fonda la relatività ristretta?
Esercizio sul calcolo dell'energia liberata durante il processo di decadimento radioattivo
Esercizio sul calcolo del fattore relativistico
Studia con noi