Potere diottrico e diottria
Che cos'è il potere diottrico e diottria?
Una lente è un oggetto costituito da un mezzo trasparente formato da due calotte sferiche (o da una calotta sferica e una parte piana) che hanno i centri di curvatura posti sullo stesso asse.
Quando la distanza tra i due vertici delle calotte sferiche diventa trascurabile si parla di lenti sottili.
Le lenti sottili si dicono convergenti se sono più spesse al centro rispetto ai bordi viceversa si diranno divergenti.
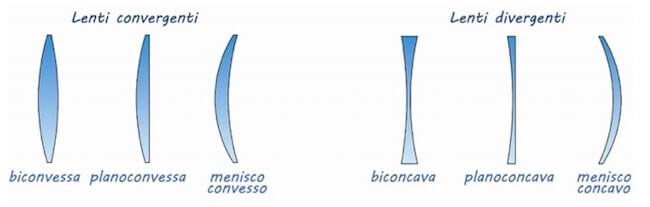
Raggi delle lenti sottili
Detti R1 e R2 i due raggi di curvatura delle calotte sferiche sinistra e destra che compongono la lente sottile le convenzioni dei segni sono i seguenti:
- lente biconvessa R1 > 0 ; R2 < 0
- Lente biconcava R1 < 0 ; R2 > 0
- Lente menisco convesso (convergente) R1 > 0 ; R2 > 0
- Lente menisco concava (divergente) R1 < 0 ; R2 < 0
Equazione dei punti coniugati per le lenti sottili
Detti:
- n l'indice di rifrazione del mezzo di cui è costituita la lente;
- p la distanza dell'oggetto rispetto alla lente;
- q la distanza dell'immagine che si forma rispetto alla lente;
- R1 e R2 i due raggi di curvatura delle calotte sferiche sinistra e destra che compongono la lente sottile;
si ha che l'equazione dei punti coniugati per le lenti sottili è espressa sotto la forma:
(1/p) + (1/q) = (n - 1) · [(1/R1) - (1/R2)]
L'equazione dei punti coniugati di una lente permette di conoscere, noti n, R1 e R2, la distanza alla quale si formerà l'immagine di un oggetto posto a distanza p dalla lente.
Distanza focale
Chiamiamo fuochi F1 ed F2 di una lente i due punti posti sull'asse ottico di una lente in cui convergono i raggi che provengono paralleli all'asse ottico stesso.
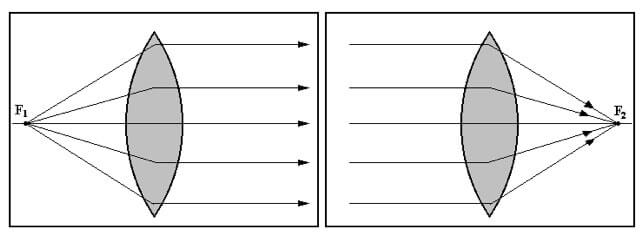
Data la simmetria del problema i fuochi sono due. La distanza tra i due fuochi e la lente sottile è detta distanza focale e viene indicata con la lettera f.
Per determinare i due fuochi dobbiamo:
- nel primo caso (grafico a sinistra) porre p = f1 (ovvero posizionare l'oggetto reale proprio sul primo fuoco) e mandare q all'infinito (formazione dell'immagine molto lontana dallo specchio, raggi paralleli all'asse ottico)
- nel secondo caso (grafico a destra) porre q = f2 e far tendere p all'infinito (raggi provenienti paralleli all'asse ottico).
In entrambi i casi si trova applicando l'equazione dei punti coniugati che:
(1/f1) + (1/f2) = (n - 1) · [(1/R1) - (1/R2)]
Ovvero i due fuochi si trovano alla stessa distanza dalla lente, tale distanza si dice allora distanza focale f della lente.
L'equazione dei punti coniugati si può scrivere allora come:
(1/p) + (1/q) = 1/f
in cui:
1/f = (n - 1) · [(1/R1) - (1/R2)]
Per una lente convergente la distanza focale sarà positiva (in quanto R1 < R2) mentre per una lente divergente la distanza focale risulterà negativa (in quanto R1 > R2).
Potere diottrico e diottria
Il potere diottrico è definito come reciproco della distanza focale di una lente sottile:
D = 1 / f
L'unità di misura del potere diottrico è la diottria.
Per le lenti convergenti il potere diottrico è positivo, in quanto f > 0; per lenti divergenti invece il potere diottrico è negativo, essendo f < 0.
Link correlati:
esercizio su lente sottile biconvessa
esercizio su lente sottile plano convessa
Come funziona un microscopio a raggi X?
Studia con noi