Pendolo semplice
Il pendolo e le leggi che lo governano
Il pendolo semplice è un sistema fisico costituito da un punto materiale di massa m appeso ad una fune di lunghezza L capace di oscillare attorno ad un punto fisso.
Le semplificazioni per lo studio di questo tipo di pendolo sono:
- il punto è privo di dimensioni:
- la fune è inestensibile ovvero mantiene fissa la distanza tra il punto materiale che oscilla e il perno attorno a cui ruota;
- la fune è priva di massa;
- non sono presenti attriti;
- gli angoli di oscillazione risultano molto piccoli.
Sotto queste ipotesi è possibile studiare da un punto di vista dinamico il moto del pendolo.
Studio del moto del pendolo
Disegniamo innanzitutto il pendolo per capire quali forze agiscono su di esso:
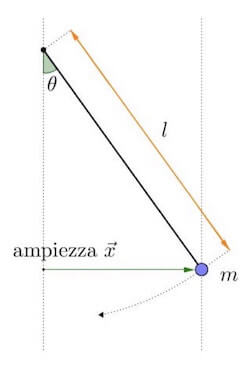
Scelto come riferimento di origine l'asse che passa dal perno cui è fissata la fune, il punto man mano che oscilla si allontana dall'origine di una distanza che chiamiamo x e che rappresenta l'ampiezza del moto di oscillazione.
Chiamiamo inoltre θ l'angolo che la fune crea con la verticale.
Sul punto agiscono due sole forze: la forza peso P diretta verso il basso e la tensione T della fune.
La forza peso può essere scomposta nelle sue due componenti parallela e perpendicolare rispetto ad un sistema di assi coordinati ortogonali con l'asse y coincidente con la direzione della fune:
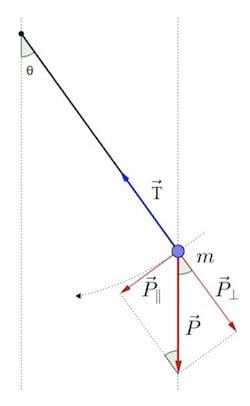
Vogliamo trovare l'accelerazione che agisce sul punto di massa m.
Applichiamo allora il secondo principio della dinamica ricordando che la somma di tutte le forze che agiscono sul punto è pari al prodotto della sua massa per l'accelerazione:
F = m∙ a
Questa equazione vettoriale per essere svolta deve essere trasformata in due equazioni scalari in cui compariranno le componenti di ogni vettore secondo il sistema di riferimento scelto, ovvero quello con l'asse y coincidente con la direzione del filo.
Allora possiamo scrivere che sull'asse orizzontale compare solamente la componente parallela della forza peso pari a:
P//= P ∙ senθ = m∙ g ∙ senθ
in cui g è l'accelerazione di gravità.
Se guardiamo bene al triangolo rettangolo che ha per ipotenusa la fune di lunghezza L e per cateto orizzontale la distanza x possiamo scrivere la relazione:
L ∙ senθ = x
ovvero:
senθ = x/L
Allora possiamo riscrivere la componente parallela della forza peso come:
P//= m ∙ g ∙ senθ = m∙ g ∙ x/L
Poiché la componente P// punta verso il lato negativo dell'asse x, allora scriviamo il secondo principio della dinamica come:
- m ∙ g ∙ x/L = m ∙ a
Semplificando m si ha che:
- g ∙ x/L = a
ovvero:
a = - (g/L) ∙ x
Dunque l'accelerazione è funzione della posizione x proprio come si ha nel moto armonico in cui l'accelerazione vale:
a = - ω2 ∙ x
in cui ω è la pulsazione del moto.
Allora possiamo scrivere
- ω2 = - g/L
da cui:
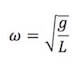
Ricordando che la pulsazione è esprimibile in funzione del periodo T di oscillazione dalla relazione:
ω = (2 ∙ π) / T
otteniamo che: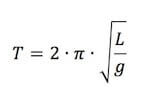
Allora possiamo concludere che per piccole oscillazioni il pendolo si comporta come un oscillatore armonico di periodo T indipendente dalla massa del pendolo, ma dipendente unicamente dalla lunghezza del filo e dall'accelerazione di gravità.
Esercizi sul pendolo
Di seguito alcuni esercizi sul pendolo.
Esercizio #1
In una certa località si contano 100 oscillazioni complete in 204 s di un pendolo lungo 1 m.
Determinare il valore della accelerazione di gravità nella località in cui si trova il pendolo.
La soluzione dell'esercizio la trovi qui: esercizio sul periodo di un pendolo.
Esercizio #2
Un pendolo semplice lungo 2 m è posto all'interno di un ascensore.
Calcolare la frequenza di oscillazione nei seguenti casi:
- l'ascensore è fermo
- l'ascensore sta salendo con un'accelerazione pari a 2 m/s2
- l'ascensore è in caduta libera
La soluzione dell'esercizio la trovi qui: calcolo della frequenza di un pendolo.
Link correlati:
Che cos'è il periodo di un pendolo?
Esercizio sul calcolo del periodo di oscillazione di un pendolo
Che cos'è l'isocronismo del pendolo?
Studia con noi