Effetto Hall
Che cos'è l'effetto Hall?
Consideriamo una lamina di spessore d percorsa da corrente ed immersa in un campo magnetico entrante nella pagina:
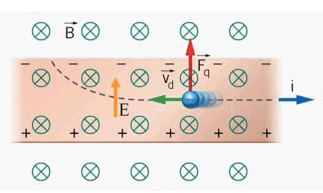
Sappiamo che il verso convenzionale della corrente corrisponde al moto delle cariche positive (nel disegno rivolto verso destra) mentre gli elettroni effettivamente si muovono in verso opposto (verso sinistra). Applichiamo adesso la regola della mano destra per determinare direzione e verso della forza di Lorentz che agisce su queste cariche in movimento con velocità perpendicolare al campo magnetico.
Il pollice della mano destra deve essere diretto come la velocità verso sinistra ma essendo la carica negativa dovremo cambiare verso esattamente opposto rispetto al verso della velocità. Quindi orienteremo il pollice della mano destra verso sinistra. L'indice rappresenta il campo magnetico ed essendo entrante nella pagina sarà rivolto verso lo schermo da cui stiamo leggendo.
Il dito medio allora perpendicolare agli altri due sarà rivolto verso l'alto restituendo direzione e verso della forza che agisce sugli elettroni deviandoli verso il bordo superiore della lamina.
Allora il bordo superiore si caricherà negativamente mentre quello inferiore positivamente. Tra le due lamine si genererà dunque una differenza di potenziale detta tensione di Hall dal nome del fisico statunitense che nella seconda metà dell'Ottocento scoprì questo fenomeno che porta il suo nome e conosciuto come effetto Hall.
Possiamo allora riassumere l'effetto Hall in questi termini: quando una lamina conduttrice è percorsa da una corrente elettrica trasversale ad un campo magnetico esterno allora le cariche tenderanno ad ammassarsi lungo uno dei due bordi della lamina generando una differenza di potenziale tra i due bordi della lamina.
Tensione di Hall
Tra i due bordi della lamina di spessore d, percorsa da elettroni di conduzione che si muovono con velocità di deriva pari a v in maniera perpendicolare ad un campo magnetico esterno di intensità B in cui è immersa la lamina si genera un campo elettrico ed una differenza di potenziale.
In particolare una volta raggiunto l'equilibrio il campo elettrico uniforme tra i due bordi della lamina sarà pari al rapporto tra la tensione tra esse, che chiameremo tensione di Hall ΔVH e lo spessore della lamina:
E = ΔVH / d
Le cariche in movimento risentono della forza di Lorentz pari al prodotto della carica dell'elettrone, e, della velocità di deriva v con cui si muovono le cariche e dell'intensità del campo magnetico B:
FL = e ∙ v ∙ B
Ma la forza è pari al prodotto della carica per il campo elettrico:
F = e ∙ E
Allora combinando le due espressioni avremo:
e ∙ E = e ∙ v ∙ B
Semplifichiamo e; sostituiamo al campo elettrico la sua espressione scritta prima in funzione della tensione di Hall:
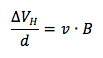
Da cui si ricava il valore della tensione di Hall:
ΔVH = v ∙ d∙ B
La tensione di Hall dunque in una lamina conduttrice percorsa da corrente ed immersa in un campo magnetico è pari al prodotto della velocità di deriva delle cariche della corrente elettrica per lo spessore della lamina per il campo magnetico.
Si può sfruttare l'effetto Hall per misurare il campo magnetico esterno a partire dalla misurazione di una differenza di potenziale che si genera tra i due bordi della lamina conduttrice.
Densità volumetrica di carica elettrica
Consideriamo una lastra metallica dotata di tre dimensioni, lunghezza larghezza e spessore percorsa da corrente I e immersa in un campo magnetico tale da poter rilevare la tensione di Hall:
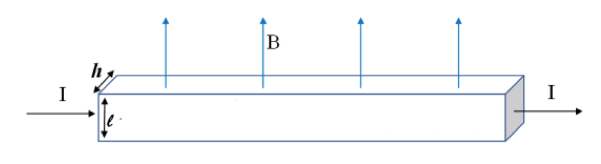
La densità volumetrica di carica elettrica ρ è la densità di carica per unità di volume della lastra. La densità volumetrica di carica è data dal rapporto tra la quantità di carica presente nel volume ed il volume stesso
ρ = Q / V
Il volume è dato dall'area trasversale della lastra h∙l per la lunghezza L della lamina:
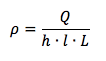
L'intensità di corrente elettrica che attraversa la lamina è pari al rapporto tra la quantità di carica Q e il tempo
i = Q / Δt
Possiamo esprimere il tempo come rapporto tra la lunghezza della lamina e la velocità di deriva delle cariche:
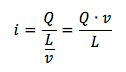
Ricaviamo adesso il valore di Q dalle due formule precedentemente ricavate per la densità volumetrica di carica e per i:
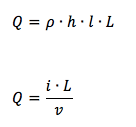
Poniamo uguali i due membri:
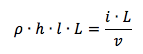
Semplifichiamo L che rappresenta la lunghezza del solido e ricaviamo ρ:
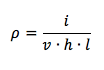
La densità volumetrica di carica dunque è pari al rapporto tra l'intensità di corrente elettrica che percorre la lamina e il prodotto tra la velocità di deriva e l'area trasversale del conduttore.
Link correlati:
Esercizi online e gratuiti sull'effetto Hall
Calcolo della densità di carica elettrica
Calcolo della velocità di deriva degli elettroni
Calcolo della corrente indotta e applicazione della legge di Lenz
Qual è l'unità di misura della corrente di spostamento?
Come funziona il selettore di velocità?
Bobina che ruota in un campo magnetico uniforme e costante e calcolo dell'intensità del campo magnetico
Studia con noi