Densità di carica elettrica
Calcolo della densità di carica elettrica ed effetto Hall
Si vuole determinare la velocità di deriva dei portatori di carica sfruttando l'effetto Hall attraverso un solido conduttore di rame di spessore l= 2,0 cm e larghezza h = 0,10 cm percorso da una corrente da 1,0 A così come mostrato in figura.
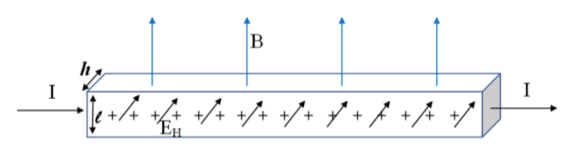
Sapendo che tra le facce del solido si rileva una tensione per unità di campo magnetico pari a 9,1 ∙ 10-7 V/T determinare la velocità di deriva degli elettroni e la densità di carica per unità di volume della lastra.
Svolgimento dell'esercizio
L'esercizio riguarda il fenomeno dell'effetto Hall per cui in una lamina conduttrice percorsa da corrente ed immersa in un campo magnetico B si genera una tensione tra due facce opposte e parallele.
Tale tensione detta di Hall è pari al prodotto della velocità di deriva delle cariche della corrente elettrica per lo spessore della lamina per il campo magnetico.
ΔVH = v ∙ h ∙ B
Il problema in particolare ci fornisce la misura della tensione per unità di campo magnetico quindi il rapporto ΔVH/B per cui la velocità di deriva dei portatori è pari a:
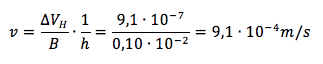
Dobbiamo adesso determinare la densità volumetrica di carica ρ cioè la densità per unità di volume della lastra. La densità volumetrica di carica è il rapporto tra la quantità di carica presente nel volume ed il volume stesso:
ρ = Q / V
Il volume è dato dall'area trasversale della lastra h∙l per la lunghezza L della lamina:
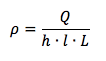
L'intensità di corrente elettrica che attraversa la lamina è pari al rapporto tra la quantità di carica Q e il tempo
i = Q / Δt
Possiamo esprimere il tempo come rapporto tra la lunghezza della lamina e la velocità di deriva delle cariche:
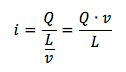
Ricaviamo adesso il valore di Q dalle due formule precedentemente ricavate per la densità volumetrica di carica e per i:
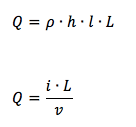
Poniamo uguali i due membri:
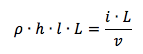
Semplifichiamo L che rappresenta la lunghezza del solido e ricaviamo ρ:
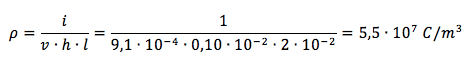
Link correlati:
Esercizi online e gratuiti sull'effetto Hall
Calcolo della velocità di deriva degli elettroni
Calcolo della costante di tempo di un circuito RC
Studia con noi