Dilatazione dei tempi
Dilatazione dei tempi: tempo proprio e tempo non proprio
Una delle conseguenze che discendono direttamente dai due postulati della relatività ristretta è quella che non esiste più un tempo assoluto uguale per tutti gli osservatori posti in sistemi di riferimento inerziali diversi tra di loro, bensì esiste un tempo proprio ed un tempo non proprio.
Inoltre a causa del fatto che la velocità di propagazione della luce è finita ed è sempre costante ed invariante in qualsiasi sistema di riferimento inerziale si assisterà ad una dilatazione dei tempi misurati tra diversi sistemi.
Si definisce tempo proprio la durata di un fenomeno quando essa è misurata in un sistema di riferimento solidale con il fenomeno stesso (in cui cioè il fenomeno avviene da fermo ed inizia e finisce nello stesso posto) e si indica con Δt.
Invece indicheremo il tempo non proprio con Δt' e questo intervallo di tempo indicherà la durata dello stesso fenomeno misurata però da chi rimane fermo rispetto al sistema in movimento in cui il fenomeno sta accadendo (in questo caso il fenomeno inizia e finisce in posti diversi a causa del moto).
Questo vuol dire che se un osservatore rimane fermo a terra mentre un altro si mette in viaggio su un'astronave a velocità costante, con velocità abbastanza prossima a quella della luce, misureranno entrambi la stessa velocità della luce e pertanto mentre per l'osservatore rimasto a terra sarà passato un certo periodo per chi si è messo in viaggio il tempo sarà trascorso in misura minore.
Dunque i due orologi dei due osservatori in moto relativo tra di loro non segneranno più lo stesso tempo.
Dimostrazione dell'esistenza del fenomeno della dilatazione dei tempi
Per dimostrare l'esistenza del fenomeno legato alla dilatazione dei tempi e della distinzione tra tempo proprio e tempo non proprio, si fa riferimento ad un orologio a luce, ovvero un dispositivo formato da due specchi piani posti parallelamente tra di loro ad una certa distanza d.
In uno dei due specchi è posta una sorgente luminosa capace di emettere luce verso lo specchio.
Una volta che il segnale luminoso parte dalla sorgente, raggiunge lo specchio opposto e torna indietro alla sorgente che è capace anche di riconoscere l'arrivo del segnale luminoso.
Visto che la velocità di propagazione del segnale luminoso è c = 3∙108 m/s, il tempo di andata e ritorno del segnale sarà pari a:
Δt = 2 ∙ d / c
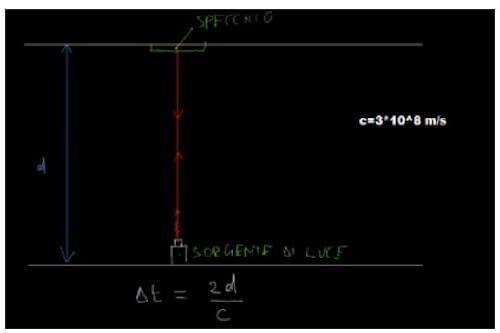
Questo tempo è quello misurato da un osservatore posto solidale con l'apparato sperimentale, quindi si tratta di tempo proprio.
Il fenomeno inizia con l'emissione del raggio luminoso dalla sorgente, raggio che poi torna indietro proprio nello stesso posto in cui è stato emesso lo stesso segnale luminoso.
Ora consideriamo un altro osservatore che si sta muovendo verso sinistra in moto rettilineo uniforme ad una certa velocità v, diretta perpendicolarmente rispetto alla congiungete sorgente specchio.
Per l'osservatore in movimento, è l'apparato sperimentale, quindi gli specchi e la sorgente, che si stanno muovendo verso destra alla sua stessa velocità v ma di verso opposto.
Per questo osservatore il raggio luminoso non si muoverà più perpendicolarmente rispetto ai due specchi, ma siccome nel frattempo l'apparato si sta spostando, la traiettoria percorsa dalla luce avrà questo andamento:
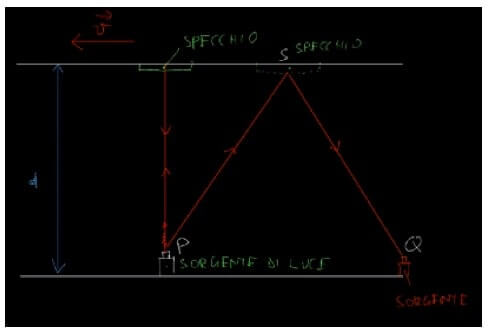
Il raggio luminoso si ricongiungerà alla sorgente in una posizione diversa da quella iniziale, una posizione che risulterà spostata verso destra, in figura indicata con la lettera Q.
Per l'osservatore in movimento, il tempo impiegato dalla luce a percorrere la traiettoria PSQ sarà data da:
Δt' = (PS + SQ) / c
Ed è proprio qui che interviene il secondo postulato della relatività ristretta per cui essendo la velocità della luce invariante rispetto a qualsiasi sistema di riferimento inerziale, anche per l'osservatore in movimento il raggio luminoso deve muoversi a velocità c, così come per l'osservatore fermo.
Essendo la distanza da percorrere nel secondo caso maggiore rispetto a quella del primo caso in quanto PS+SQ > 2∙d ciò porta alla conseguenza diretta che Δt' > Δt ovvero il tempo misurato dall'osservatore in movimento risulta dilatato rispetto a quello misurato dall'osservatore fermo.
Il fenomeno sembra durare di più nel caso in cui inizia e finisce in posti diversi.
Le distanze PS e SQ sono uguali, essendo il triangolo PSQ isoscele.
Per calcolare PS facciamo riferimento al secondo osservatore in movimento che vede lo specchio muoversi verso destra dalla sua posizione iniziale S0 e raggiungere la posizione S.
Tale distanza è pari a:
S0S = v ∙ Δt' / 2
essendo Δt' il tempo totale del percorso, va diviso per due la distanza.
La distanza tra P e S0, che avevamo chiamato d inizialmente, è quella misurata dall'osservatore fermo e vale:
Δt = 2 ∙ d / c = 2 ∙ PS0 / c
da cui:
PS0 = c ∙ Δt / 2
Infine la distanza PS è quella percorsa dalla luce che si muove alla sua velocità c nell'intervallo di tempo Δt'/2 rispetto all'osservatore in movimento:
PS = c ∙ Δt' / 2
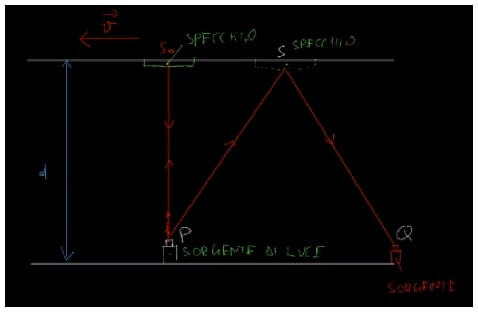
Applichiamo ora il teorema di Pitagora al triangolo rettangolo PS0S:
PS2 = PS02 + S0S2
Sostituiamo:
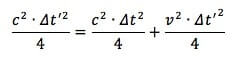
Moltiplichiamo ambo i membri per 4 e portiamo i termini con Δt' a primo membro:
c2 ∙ Δt'2 = c2 ∙ Δt2 + v2 ∙ Δt'2
c2 ∙ Δt'2 - v2 ∙ Δt'2 = c2 ∙ Δt2
Ricaviamo adesso Δt':
(c2 - v2) ∙ Δt'2 = c2 ∙ Δt2
Δt'2 = (c2 ∙ Δt2) / (c2 - v2)
Raccogliamo c2 a denominatore:
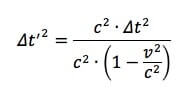
Semplifichiamo c2 ed estraiamo la radice quadrata:
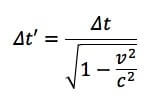
Questa formula fondamentale lega il tempo non proprio Δt', cioè quello misurato per un osservatore che vede iniziare e finire un fenomeno in due punti diversi, al tempo proprio Δt ovvero l'intervallo di tempo tra due eventi misurato da un osservatore che li vede accadere nello stesso punto.
Il paradosso dei gemelli è un esperimento ideale proposto da Einstein che mette ben in evidenza questo aspetto nuovo del tempo inteso in senso relativo e non più assoluto come invece lo si era creduto sin dai tempi di Aristotele, Newton e Galileo.
Prove sperimentali della dilatazione dei tempi
Innumerevoli sono le prove sperimentali che provano il fenomeno della dilatazione dei tempi.
Essendo molto difficile raggiungere velocità prossime a quelle della luce per corpi macroscopici (si pensi che la massima velocità di una sonda costruita dall'uomo e lanciata nello spazio è stata di 70000 m/s ovvero una frazione irrilevante rispetto a 300000000 m/s della luce) è molto più semplice lavorare con particelle subatomiche che possono più facilmente raggiungere le velocità relativistiche per cui è possibile evidenziare il fenomeno della dilatazione dei tempi.
Ad esempio, al Cern di Ginevra è possibile accelerare particelle a velocità molto elevate, prossime a quella della luce, o in maniera naturale è molto utile riportare il caso dei mesoni μ detti muoni.
Queste particelle si creano dall'interazione dei raggi cosmici, particelle cariche ad alta energia, che arrivano dallo spazio e vengono filtrate dagli alti strati della nostra atmosfera.
Questa interazione tra raggi cosmici e atomi dell'atmosfera danno origine ai muoni, particelle subatomiche che decadono spontaneamente in un tempo di 2,2∙10-6 s.
Anche ammettendo che i muoni si potessero muovere alla velocità della luce c, la distanza che potrebbero percorrere dal punto in cui si originano risulterebbe pari a:
d = c ∙t = 3∙108 ∙ 2,2∙10-6 = 660 m
Dunque i muoni dopo soli 660 m dovrebbero sparire essendo decaduti. Tuttavia i muoni riescono ad arrivare sino al suolo terrestre e possono anche essere rilevati.
Perché avviene ciò? Semplice! Le velocità con cui viaggiano i muoni sono prossime a quelle della luce ovvero pari al 99,92% di c.
A tali velocità l'effetto relativistico di dilatazione dei tempi diventa non più affatto trascurabile.
Dunque la vita media dei muoni si allunga ed hanno il tempo di arrivare sino al suolo terrestre percorrendo ben più dei 660 m previsti dalla fisica classica.
Esercizio 1
Una stella è situata a 100 anni luce dalla Terra.
Quanto tempo impiega la luce che parte da quella stella a raggiungere il nostro pianeta?
Quanto tempo impiegherebbe, nel proprio sistema di riferimento, un astronauta se viaggiasse ad una velocità di 0,999∙c?
Esercizio 2
In un acceleratore di particelle si sta facendo viaggiare una particella elementare ad una velocità v tale da allungare del 30 % la sua vita media.
Di quanto deve aumentare in percentuale la velocità della particella se si vuole portare la dilatazione del tempo di vita media al 60%?
Lo svolgimento dell'esercizio lo trovi qui: dilatazione del tempo di vita media di una particella.
Lo svolgimento lo trovi qui: esercizio sulla dilatazione dei tempi.
Link correlati:
Cosa afferma la legge della contrazione delle lunghezze?
Che cos'è la massa relativistica?
Esercizio sulla frequenza cardiaca perpecita da un astronauta e relatività ristretta
Che cos'è la quantità di moto relativistica?
Esercizio sul tempo proprio e sul tempo non proprio
Spiegazione dell'esperimento di Michelson e Morley
Che cos'è l'equazione di campo di Einstein?
Studia con noi