Velocità angolare
Che cos'è e come si calcola la velocità angolare?
Consideriamo un punto materiale che si muove di moto circolare lungo una circonferenza, ad esempio il moto di un satellite artificiale intorno alla Terra.
Poiché; le dimensioni del satellite sono molto inferiori rispetto a quelle della sua traiettoria circolare possiamo approssimare il moto come quello di un punto materiale per semplicità.
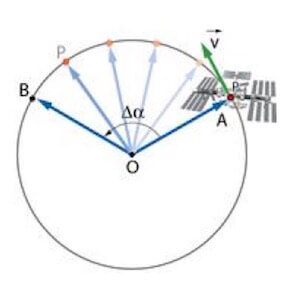
Lungo la sua orbita, il satellite percorrerà un arco AB che corrisponde ad un angolo al centro percorso o meglio detto "spazzato"![]() .
.
Detto tale angolo spazzato Δα e Δt il tempo impiegato dal raggio vettore a spazzare l'angolo, si definisce velocità angolare ω il rapporto tra Δα e Δt:
ω = Δα / Δt
L'unità di misura nel Sistema Internazionale è il radiante al secondo [rad/s].
La velocità angolare rappresenta dunque la rapidità con cui il raggio vettore spazza l'angolo al centro in un determinato intervallo di tempo.
Velocità angolare nel moto circolare uniforme
Se la velocità angolare è costante allora parliamo di moto circolare uniforme; in esso il raggio vettore spazza angoli uguali in tempi uguali.
In particolare detto T l'intervallo di tempo necessario a percorrere un angolo giro completo (2·π radianti = 360°) la velocità angolare risulta:
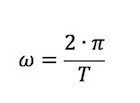
Nel moto circolare uniforme l'angolo spazzato dal raggio vettore è direttamente proporzionale all'intervallo di tempo impiegato a spazzarlo.
La formula inversa per ricavare il periodo T a partire dalla velocità angolare è:
T = 2 · π / ω
Velocità angolare nel moto circolare uniformemente accelerato
Nel moto circolare uniformemente accelerato il vettore velocità tangenziale non ha più modulo costante, questo vuol dire che il punto sta ruotando incrementando (o decrementando) la propria velocità.
Il punto sarà dunque soggetto ad un'accelerazione tangenziale costante (perché; il moto è di tipo uniforme) che ha lo stesso verso della velocità.
Il raggio vettore spazzerà a sua volta con velocità angolare sempre crescente (o decrescente) l'angolo al centro, allora si parla di accelerazione angolare solitamente indicata con α.
Visto che l'accelerazione tangenziale è costante anche l'accelerazione angolare è costante e accelerazione angolare media e istantanea coincidono:
α = Δω / Δt
ed ha come unità di misura i rad/s2.
Le leggi del moto circolare uniformemente accelerato sono molto simili a quelle del moto rettilineo uniformemente accelerato con la differenza che qui si considera un'accelerazione angolare α, un angolo iniziale θ0 e finale θ ed una velocità angolare iniziale ω0 e finale ω:
ω = ω0 + α · t
θ = ½ · α · t2 + ω0 · t + θ0
2 · α · (θ - θ0) = ω2 - ω02
Esercizio sul calcolo della velocità angolare
Calcolare velocità tangenziale ed accelerazione centripeta di un elettrone che ruota attorno al nucleo di un atomo di idrogeno, assumendo che l'orbita sia circolare di raggio 5 · 10-11 m e che il periodo sia pari a 1,5 · 10-16 s.
Calcolare infine la velocità angolare.
La soluzione la trovi qui: esercizio sul calcolo della velocità angolare.
Esercizio sul moto circolare uniformemente accelerato
Un punto materiale si sta muovendo di moto circolare uniformemente accelerato lungo una circonferenza di raggio 2 m.
La sua velocità tangenziale viene misurata all'istante t e vale 1 m/s.
All'istante t + 3s il corpo ha percorso 5 m.
Determinare:
1) l'accelerazione angolare
2) la velocità angolare dopo 5 s
3) l'accelerazione centripeta dopo 2 s
4) l'accelerazione tangenziale
5) il numero di giri fatti dopo 10 s
La soluzione la trovi qui: esercizio sul moto circolare uniformemente accelerato.
Altri esercizi
Li trovi qui: esercizi sulla velocità angolare.
Studia con noi