Moto circolare uniforme
Come avviene il moto circolare uniforme
Quando la traiettoria seguita da un punto materiale non è rettilinea, bensì curvilinea, si parla di moto curvilineo.
Tra i moti curvilinei assume notevole importanza il moto caratterizzato da una traiettoria circolare, che è il moto seguito ad esempio dalle pale di un ventilatore che girano, dalle ruote di un'automobile o da un dvd che è posto in rotazione all'interno di un lettore.
Tali esempi fanno riferimento dunque al moto circolare, che se caratterizzato da velocità di modulo costante allora si dirà moto circolare uniforme.
Velocità nel moto circolare uniforme
Il vettore velocità tangenziale è un vettore che rappresenta la velocità con cui si muove un punto lungo una circonferenza.
Esso ha la direzione della tangente alla traiettoria nella posizione che il punto occupa in quell'istante, cioè perpendicolare al raggio della traiettoria circolare che passa per quel punto.
Se il modulo della velocità tangenziale rimane sempre costante nel moto circolare uniforme, quello che cambia istante per istante è invece la direzione:
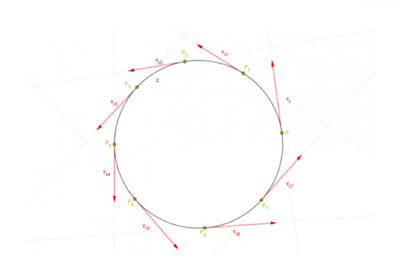
Nella figura sopra sono rappresentate diverse posizioni assunte dal punto lungo la sua rotazione e per ogni posizione assunta è stato disegnato il vettore tangente che ne rappresenta la velocità tangenziale.
Accelerazione nel moto circolare
In un moto circolare uniforme il vettore velocità tangenziale mantiene costante il proprio modulo lungo tutto la circonferenza, pertanto il corpo percorre archi uguali in tempi uguali.
Se però la direzione della velocità cambia istante per istante è necessario introdurre il concetto di accelerazione centripeta, che interviene nella variazione di direzione del vettore velocità.
L'accelerazione centripeta è un vettore perpendicolare alla velocità e diretta verso il centro, lungo la direzione del raggio:
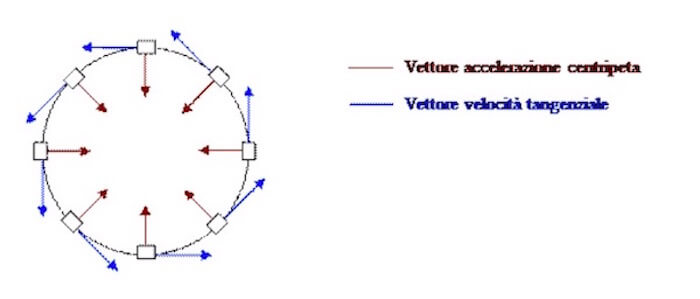
Se il moto non è uniforme ma il modulo del vettore velocità tangenziale cambia nel tempo allora si parlerà di accelerazione tangenziale, che ha la stessa direzione del vettore velocità:
Nella figura sono rappresentati i due vettori accelerazione centripeta e tangenziale, si può notare come essi siano perpendicolari tra di loro.
Periodo e frequenza
In un moto circolare il punto in rotazione occuperà nuovamente la propria posizione iniziale dopo aver compiuto un giro completo.
Si definisce periodo e si indica con T l'intervallo di tempo necessario a svolgere un giro completo della propria traiettoria. Esso si misura in secondi.
Strettamente connessa alla definizione di periodo è quella di frequenza, f; essa rappresenta quanti giri il punto compie in un secondo e si misura in hertz [Hz].
La frequenza rappresenta dunque l'inverso del periodo:
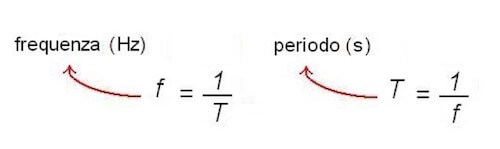
Velocità tangenziale e velocità angolare
Detti R il raggio della traiettoria circolare e T il periodo del modo, la velocità tangenziale V si calcola come il rapporto tra lo spazio percorso ed il tempo impiegato a percorrere tale spazio.
Ricordando che la lunghezza di una circonferenza è data da 2·π·R e che il tempo impiegato a compiere un giro completo è proprio il periodo T allora:
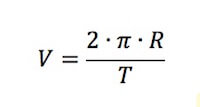
Sfruttando la relazione tra periodo e frequenza si ha che:
V = 2 · π · R · f
La velocità tangenziale si misura in m/s.
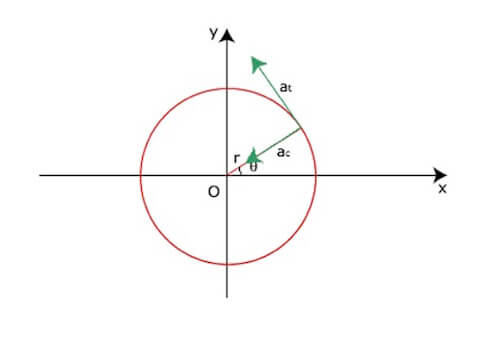
Il moto circolare è anche caratterizzato anche da un'altra velocità, quella definita velocità angolare ω, che rappresenta l'angolo spazzato dal punto che ruota rispetto al tempo.
Ora, siccome un giro completo corrisponde a 360°, che in radianti corrisponde ad un angolo di 2·π allora la velocità angolare ω vale:
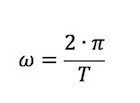
Oppure espressa in termini di frequenza:
ω = 2 · π · f
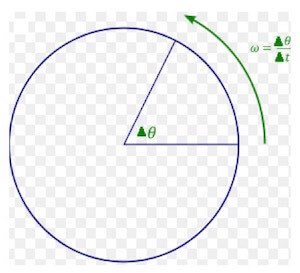
Come si evince dalla figura la velocità angolare è il rapporto tra l'angolo spazzato Δθ e l'intervallo di tempo impiegato a spazzarlo.
La velocità angolare si misura in rad/s.
In un moto circolare uniforme sia la velocità tangenziale sia quella angolare risultano costanti.
A partire dalle formule di velocità tangenziale ed angolare vediamo ora di ricavare tutte le formule inverse possibili:
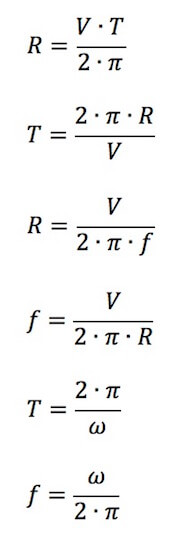
Riguardiamo attentamente le formule che permettono di calcolare velocità tangenziale ed angolare:
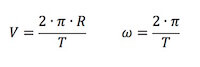
Le due formule possono essere legate tra di loro attraverso la seguente espressione:
V = ω · R
da cui
ω = V/R
e
R = V / ω
Accelerazione centripeta
Come già detto, nel moto circolare uniforme esiste un'accelerazione istantanea costante diretta verso il centro e perpendicolare alla velocità tangenziale punto per punto della traiettoria.
Tale accelerazione si dice centripeta (cioè diretta verso il centro) ed il modulo vale:
ac = V2 / R
l'unità di misura è il m/s2.
Combinando le formule che abbiamo visto otteniamo:
ac = ω2 · R
da cui si ottengono le formule inverse per il raggio:
R = V2 / ac
e
R = ac / ω2
Le formule per le velocità tangenziale ed angolare sono invece:
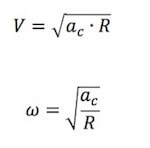
Grafico spazio-tempo
Il moto circolare è un moto che avviene in un piano bidimensionale.
Se studiamo l'andamento della proiezione del punto che ruota lungo la circonferenza, proiettando istante dopo istante la sua posizione lungo gli assi x e y otteniamo due moti periodici, ovvero la proiezione del punto continuerà ad oscillare tra i due estremi del diametro lungo l'asse x e y.
Si definisce moto armonico la proiezione su un diametro del moto circolare uniforme.
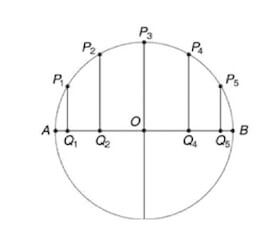
L'andamento del punto lungo i due assi sarà di tipo sinusoidale o cosinusoidale: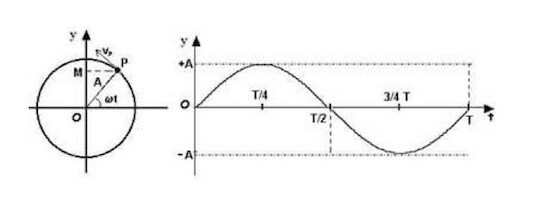
Esercizi sul moto circolare uniforme
Se ti interessano li trovi qui: esercizi sul moto circolare uniforme.
Link correlati:
Quali sono le formule del moto circolare uniforme?
Studia con noi