Frequenze di un'onda stazionaria
Esercizio sulle frequenze di un'onda stazionaria
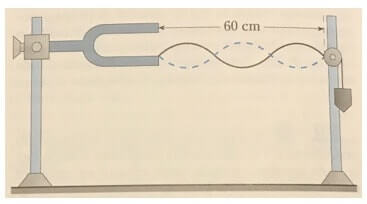
Una corda possiede densità lineare pari a μ = 2 ∙ 10-3 kg/m ed è lunga 60 cm.
La corda si trova tra due estremi costituiti da un diapason da un lato e da un peso sospeso tramite carrucola dall'altro in modo tale da farla stare in tensione.
Determinare la massa che si trova sospesa tale per cui se il diapason vibra a 400 Hz allora la corda oscillerà alla terza armonica.
Svolgimento dell'esercizio
Detta v la velocità di propagazione dell'onda ed L la lunghezza della corda in cui l'onda si sta propagando, le frequenze dell'onda stazionaria n-esima si trovano secondo la seguente relazione:
fn = (n · v) / (2 · L)
con n = 1,2,3…
Nel problema in particolare viene detto che la corda sta vibrando nella frequenza corrispondente alla sua terza armonica, per cui n=3.
Sappiamo inoltre (vedi paragrafo sulle onde trasversali e onde longitudinali) che la velocità di propagazione di un'onda trasversale lungo una corda tesa vale:
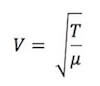
cioè la velocità di propagazione dell'onda nella corda dipende dalla tensione T a cui è sottoposta la corda e dalla sua densità lineare μ. Non dipende invece dalla frequenza dell'onda.
Per cui sapendo che f3 = 400 Hertz allora:
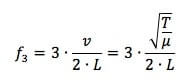
Ricaviamo dunque T. Eleviamo al quadrato ambo i membri:
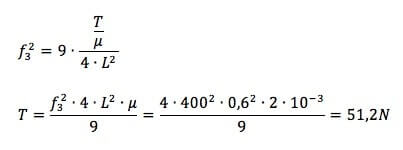
Questa tensione corrisponde alla forza peso con cui la massa sospesa è attratta verso il basso per cui:
T = m ∙ g
Da questa relazione ricaviamo la massa del corpo sospeso:
m = T/g = 51,2/9,8 = 5,2 kg
Studia con noi