Onde trasversali e onde longitudinali
Che cosa sono le onde trasversali e le onde longitudinali?
Un'onda è una perturbazione che si propaga nello spazio trasportando energia ma non materia.
L'onda è emessa da una sorgente e può sostanzialmente essere di due tipi: meccanica o elettromagnetica.
Le onde meccanica hanno bisogno di un mezzo per propagarsi mentre quelle elettromagnetiche no.
Sono esempi di onde meccaniche le onde del mare, le onde prodotte da una corda tesa, il suono, le onde sismiche.
Sono invece onde elettromagnetiche i raggi infrarossi, la luce visibile i raggi X, i raggi UV, ecc.
Ora, a seconda della posizione reciproca delle direzioni di vibrazione e di propagazione di un'onda distinguiamo onde trasversali e onde longitudinali.
Nelle onde longitudinali la direzione di oscillazione coincide con quella di propagazione. È il caso di una molla che si comprime e si espande:
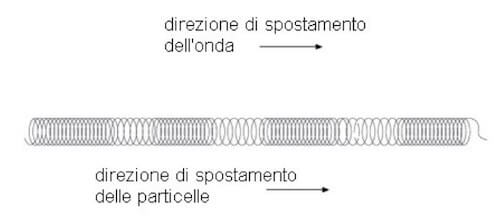
Le onde trasversali sono invece quelle onde in cui l'oscillazione avviene perpendicolarmente rispetto alla direzione di propagazione:
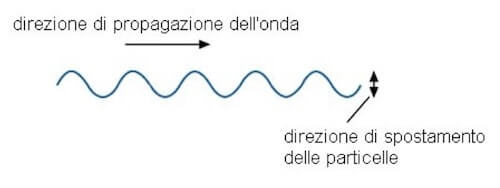
Propagazione delle onde meccaniche
La velocità di propagazione di un'onda dipende dalle proprietà del mezzo in cui si propaga.
In particolare si può dimostrare ciò prendendo il caso di un'onda trasversale che si propaga lungo una corda tesa ideale.
Ipotizziamo che un'onda trasversale stia attraversando una corda deformandola al suo passaggio:
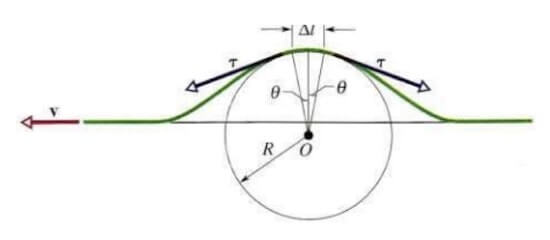
L'elemento Δl di corda deformata sente una forza di tensione T da ambedue i lati al passaggio dell'onda.
Le componenti orizzontali dei due vettori T si annullano in quanto ogni punto della corda oscilla soltanto su un piano perpendicolare rispetto alla direzione di propagazione dell'onda trasversale.
Per cui la risultante dei due vettori è la somma delle loro componenti verticali:
Tris = 2 ∙ T ∙ senθ
Poiché gli angoli sono molto piccoli, possiamo approssimare il seno dell'angolo con l'angolo stesso, per cui:
Tris = T ∙ 2 ∙ θ
Sappiamo che per un settore circolare, l'angolo è dato dal rapporto tra la lunghezza dell'arco del settore ed il raggio della circonferenza:
Tris = T∙Δl/R
Introduciamo adesso la grandezza μ che rappresenta la densità lineare della corda, ovvero il rapporto tra la sua massa e la sua lunghezza:
μ = m / L
L'unità di misura della densità lineare è kg/m.
Se l'arco di lunghezza Δl possiede massa Δm allora possiamo scrivere questa massa come:
Δm = mdell'arco Δl = μ ∙ Δl
Infine possiamo pensare all'elemento di corda Δl come se si stesse muovendo di moto circolare uniforme lungo una circonferenza di raggio R, per cui esso è sottoposto ad accelerazione centripeta pari a:
a = V2 / R
In cui V è la velocità di propagazione dell'onda nella corda.
Applicando la seconda legge di Newton per cui:
F = mdell'arco Δl ∙ a
essendo F la risultante delle forze Tris otteniamo:
T∙Δl /R= μ ∙ Δl ∙ V2 / R
Possiamo semplificare sia R sia Δl ad ambo i membri e otteniamo dunque che la velocità di propagazione di un'onda trasversale lungo una corda tesa vale:
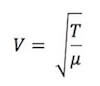
Cioè la velocità di propagazione dell'onda nella corda dipende dalla tensione T a cui è sottoposta la corda e dalla sua densità lineare. Non dipende invece dalla frequenza dell'onda.
Esercizio #1
La velocità di propagazione di un'onda trasversale lungo una corda tesa è di 30 m/s.
Sapendo che la tensione a cui è sottoposta la corda è di 90 N, determinare la densità lineare della corda.
Determinare infine la lunghezza d'onda della sapendo che la frequenza dell'onda è di 150 Hz.
Lo svolgimento dell'esercizio lo trovi qui: calcolo della densità lineare di una corda.
Esercizio #2
La corda di un violino è composta di un materiale che possiede densità lineare di 2,5 g/m ed è sottoposta ad una tensione di 10 N.
Determinare la velocità dell'onda che si propaga lungo la corda e la frequenza sapendo che la lunghezza d'onda vale 14,4 cm.
Lo svolgimento dell'esercizio lo trovi qui: calcolo della velocità di propagazione di un'onda trasversale.
Studia con noi