Esercizio sulla rifrazione
Esercizio svolto sulla reazione rifrazione
Un raggio di luce monocromatico incide su di una lastra piana a facce piane parallele di un certo spessore s.
La lastra è composta da un materiale caratterizzato da un indice di rifrazione pari a 1,2247.
Il raggio arriva a incidere la lastra con un angolo di 60° rispetto alla normale alla superficie e ne emerge spostato di una distanza pari a 5 cm.
Determinare lo spessore della lastra.
Svolgimento dell'esercizio
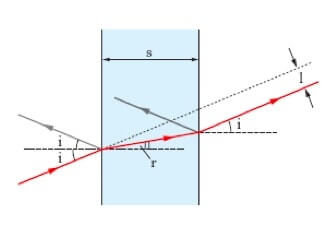
Quando il raggio di luce attraversa la lastra, il raggio emergente risulterà parallelo a quello incidente.
È semplice dimostrare ciò applicando due volte la legge di Snell al passaggio del raggio dall'aria (mezzo 1) alla lastra (mezzo 2) e di nuovo all'aria (mezzo 3).
Poiché l'indice di rifrazione dell'aria è 1, avremo:
n1 = n3 = 1
dunque:
n1 ∙ sen i = n2 ∙ sen r = n3 ∙ sen i'
Da cui:
sen i = sen i'
e quindi:
i = i'
Il raggio emergente come si evince dal testo del problema risulta spostato di una quantità l pari a 5 cm.
l = 5 cm (spostamento laterale del raggio).
Calcoliamo anzitutto l'angolo di rifrazione r:
sen i / sen r = n2 / n1
Da cui:
r = arcsen (sen 60 / n2)
r = arcsen (sen 60 / 1,2247) = 45°
Calcoliamo la lunghezza b del raggio rifratto che attraversa diagonalmente la lastra.
Considerando lo spessore s della lastra come cateto orizzontale, vale la relazione:
b ∙ cos r = s
da cui:
b = s / cos r
Considero adesso il triangolo rettangolo che ha come ipotenusa b, lunghezza del raggio rifratto all'interno della lastra, e come cateto verticale l:
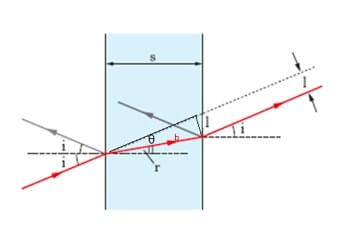
Il triangolo è sicuramente rettangolo in quanto le due rette in cui giacciono raggio incidente e raggio emergente sono parallele.
L'angolo acuto θ non è altro che la differenza tra l'angolo di incidenza i di 60° e l'angolo di rifrazione r di 45°:
θ = 60° - 45° = 15° (angoli alterni interni).
Dunque vale la relazione:
b ∙ sen θ = l
mettendo a sistema quest'ultima con
b = s/cos r
otteniamo:
s/cos r ∙ sen θ = l
Da cui:
s = l ∙ cos r / sen θ
Pertanto:
s = 5 ∙ cos 45 / sen 15 = 13,66 cm
Quindi lo spessore della lastra è di 13, 66 cm.
Link correlati:
Che cos'è la rifrattometria?
Studia con noi