Reticolo di diffrazione
Che cos'è il reticolo di diffrazione?
Un reticolo di diffrazione è un sistema costituito da un numero N di fenditure, ognuna di larghezza a, poste tutte alla stessa distanza d tra di loro impiegato per separare i colori della luce.
La distanza d tra due fenditure consecutive si dice passo del reticolo, per cui la larghezza complessiva del reticolo considerando le N fenditure è pari a:
L = N ∙ d
Il passo del reticolo deve essere confrontabile con la lunghezza d'onda della luce incidente; valori tipici possono essere:
d = 2,5 μm
N = 104
per una larghezza complessiva quindi di :
L = 2,5 cm
Solitamente un reticolo di diffrazione è realizzato incidendo con precisione delle scanalature a distanza costante tra di loro su una lastra di vetro ottico.
Un esempio di reticolo di diffrazione può essere considerata la superficie di un compact disc, le scanalature presenti sulla sua superficie producono infatti dei fenomeni di riflessione della luce.

Figura di diffrazione
Quando un'onda piana investe il reticolo di diffrazione, ogni singola fenditura si comporta come nuova sorgente di onde sferiche.
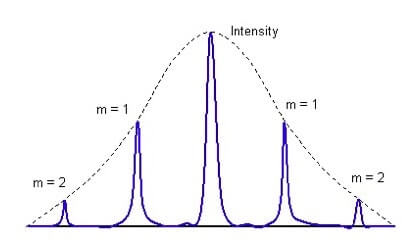
I fasci così diffratti, interferendo tra di loro, determinano una figura di diffrazione costituita da un massimo centrale, detto massimo di ordine 0, da massimi del primo ordine, del secondo ordine ecc.
L'ordine dei massimi si indica con la lettera m per cui per m= 0 avremo il massimo centrale, per m = ± 1 i due massimi laterali , per m = ± 2 quelli ancora successivi e così via.
L'equazione del reticolo di diffrazione
L'equazione che descrive la distribuzione delle frange dei massimi prodotta da un reticolo è:
senθ = m · λ / d
In cui:
- θ è l'angolo formato dalla direzione del raggio diffratto rispetto alla normale al piano del reticolo;
- m è l'ordine dei massimi;
- λ è la lunghezza d'onda della radiazione incidente utilizzata;
- d è il passo del reticolo.
L'equazione del reticolo permette dunque di calcolare le direzioni per le quali risulta massima l'intensità della radiazione per effetto dell'interferenza di tutte le onde diffratte.
Per calcolare l'ordine massimo che si può ottenere nella figura di diffrazione generata da un reticolo, bisogna ricordare che la funzione seno non può assumere valori maggiori di 1:
senθ ≤ 1
Allora risulta che:
m · λ / d ≤ 1
ovvero:
m ≤ d / λ
Detta a la larghezza di ogni singola fenditura inoltre si può ricavare la relazione che lega l'ordine m' del primo massimo principale mancante con il passo del reticolo e la larghezza stessa di ogni fenditura:
m' = d / a
Larghezza angolare
Per calcolare la larghezza angolare di un massimo principale si utilizza la seguente formula:
Δθm = 2 · λ / (L · cosθm)
in cui:
- λ è la lunghezza d'onda della radiazione incidente utilizzata;
- L è la larghezza complessiva del reticolo;
Dunque a parità di passo d di un reticolo, se il reticolo ha una larghezza maggiore, avrà un maggior numero di fenditure e più stretti saranno i massimi principali.
Link correlati:
Link correlati:
Diffrazione dei raggi X: spiegazione e definizione del fenomeno
Esercizio svolto e commentato sul reticolo di diffrazione
Esercizio sul calcolo del numero di fenditure di un reticolo di diffrazione
Come funziona un microscopio a raggi X?
Studia con noi