Equilibrio tra forza peso e forza elettrica
Esercizio sull'equilibrio tra forza peso e forza elettrica
Una bolla di sapone è sospesa in aria senza cadere. La densità del sapone vale 1,1∙103 kg/m3 e lo spessore della bolla è pari a 6,0∙10-5 m.
Sapendo che il raggio esterno della bolla misura 1 cm e che il campo elettrico presente sulla sua superficie è pari a 11 kV/m determinare quale campo elettrico bisogna applicare dall'esterno affinché la bolla rimanga sospesa in aria.
Svolgimento dell'esercizio
La bolla di sapone è una sfera cava dotata di raggio interno ed esterno. Per rimanere sospesa in equilibrio vi deve essere uguaglianza tra la forza peso diretta verso il basso e la forza elettrica da applicare tramite un campo esterno diretta verso l'alto.
Determiniamo dapprima la carica presente sulla sfera.
Sappiamo che tutta la carica si è distribuita sulla superficie esterna della bolla conduttrice, per cui per il teorema di Coulomb possiamo scrivere che il campo elettrico presente sulla superficie è pari al rapporto tra la densità superficiale di carica e la costante dielettrica nel vuoto:
E = |σ| / ε
Allora la densità superficiale di carica in modulo varrà:
σ = E ∙ ε0
e siccome la densità superficiale di carica altro non è che il rapporto tra la carica complessivamente presente sulla sfera e la superficie della sfera stessa allora avremo:
Q / (4 ∙ π ∙ R2) = E ∙ ε0
Quindi la carica Q risulterà pari a:
Q = 4 ∙ π ∙ R2 ∙ E ∙ ε0
Q = 4 ∙ π ∙ (10-2)2 ∙ 11 ∙ 103 ∙ 8,85 ∙ 10-12
Q = 1,2 ∙ 10-10 C
Ora per sostenere la sfera in equilibrio bisogna applicare un campo elettrico esterno tale per cui la forza elettrica derivante da questo campo eguagli la forza peso della sfera.
Per calcolare la forza peso però abbiamo bisogno di conoscere la massa della bolla.
Ricordando che si tratta di una sfera cava ma dotata di raggio interno ed esterno e che la densità è data dal rapporto tra massa e volume si ottiene che:
m= ρ ∙ V
in cui:
- ρ è la densità del sapone;
- V il volume del guscio.
Per calcolare il volume basta sottrarre il volume della sfera esterna, utilizzando la misura del raggio esterno, meno la misura del volume interno.
m = ρ ∙ (4/3) ∙ π ∙ (R3 - r3)
In cui:
R = 1 cm = 10-2 m
e
r = 1 - 6,0∙10-5 m = 9,94 ∙ 10-3 m
Ricordiamo che la forza elettrica è data dal prodotto del campo elettrico per la carica elettrica:
Felettrica = Fpeso
E ∙ q = m ∙ g
Da cui:
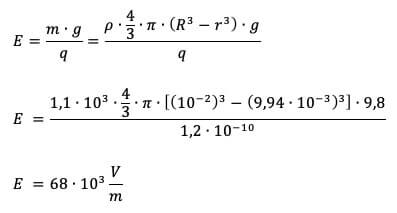
Link correlati:
Come può essere dimostrato il teorema di Gauss?
Principali applicazioni del teorema di Gauss?
Che cos'è il pozzo di Faraday?
Studia con noi