Trasformazioni di Galileo
Che cosa sono le trasformazioni di Galileo?
Ogni evento che accade in un determinato sistema di riferimento, può essere caratterizzato dalle 3 coordinate spaziali x, y e z e dalla coordinata temporale t.
Le trasformazioni di Galileo riguardano proprio la trasformazione di queste quattro coordinate spazio temporali quando, ad osservare lo stesso evento, ci si pone in un sistema di riferimento inerziale, che si muove cioè di moto rettilineo uniforme rispetto al primo.
Le nuove coordinate saranno qui indicate come x', y', z' e t'.
Innanzitutto tali tipi di trasformazioni presuppongono che il tempo scorra allo stesso modo nei due sistemi di riferimento, indipendentemente dalla velocità con cui si muove l'uno rispetto all'altro, per cui:
t' = t
Questa ipotesi, vedremo, sarà radicalmente stravolta dalla teoria della relatività di Einstein.
Se il sistema di riferimento S' si muove a velocità costante v rispetto al sistema di riferimento S, lungo le direzioni comuni degli assi x e x', dopo un certo tempo t le nuove coordinate spazio temporali nel nuovo sistema di riferimento saranno dunque:
x' = x - v ∙ t
y' = y
z' = z
t' = t
Grandezze varianti ed invarianti
Quando si passa da un sistema di riferimento ad un altro inerziale, ci sono alcune grandezze che rimangono invariate mentre altre varieranno necessariamente.
Le grandezze fisiche che rimangono invariate sono, come già detto, il tempo, le lunghezze, le masse, le forze e le accelerazioni.
Risultano invece grandezze varianti lo spostamento, o variazione di spazio, Δs e la velocità.
Dimostriamo adesso che le lunghezze sono grandezze invarianti rispetto alle trasformazioni di Galileo.
Dato due punti M e N nel sistema di riferimento S, la loro lunghezza d è il segmento riportato in figura:
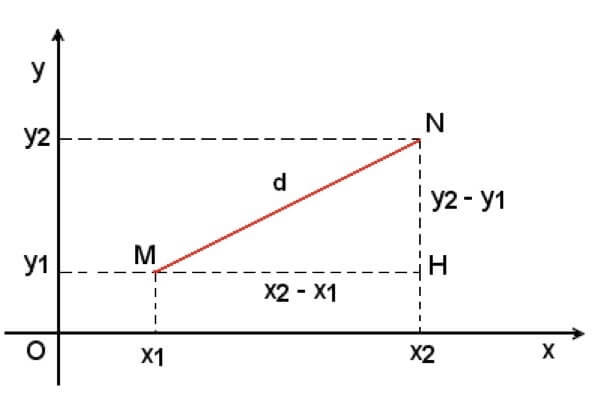
La loro distanza MN vale:
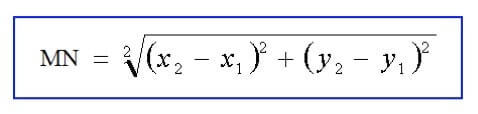
Proviamo adesso a calcolare la stessa distanza ponendoci in un sistema di riferimento inerziale S', che si sta muovendo a velocità costante v, ad un certo istante di tempo t.
Sappiamo che per le trasformazioni di Galileo, le nuove coordinate x e y dei punti saranno:
x2' = x2 - v∙t
x1' = x1 - v∙t
y2' = y2
y1' = y1
Allora:
(x2' - x1') = (x2 - v∙t) – (x1 - v∙t) = x2 - v∙t – x1 + v∙t = x2 – x1
(y2' - y1') = (y2 - y1)
E dunque risulterà
MN' = MN
Dimostriamo ora che invece la variazione di spazio è una grandezza che cambia nel passaggio da un sistema di riferimento ad un altro.
Durante l'intervallo di tempo considerato Δt, il nuovo sistema di riferimento inerziale si sarà spostato di una distanza pari a (v ∙ Δt).
Per cui allo spostamento del corpo rilevato nel primo sistema di riferimento, bisogna aggiungere la quantità prima citata perché a sua volta il nuovo sistema di riferimento si è spostato:
Δs = Δs' + v ∙ Δt
Cioè
Δs' = Δs - v ∙ Δt
Legge d composizione di spostamento e velocità
Vediamo quali sono le formule che legano lo spostamento e la velocità di un punto se calcolati in un sistema di riferimento o in un altro inerziale rispetto al primo.
Detto Δsr lo spostamento compiuto da un punto materiale all'interno di un sistema di riferimento e Δst lo spostamento che invece compie un sistema di riferimento inerziale, cioè in moto con velocità costante rispetto al primo, lo spostamento del punto rispetto al secondo sistema, quello in moto, risulterà pari a:
Δs = Δsr + Δst
Tale equazione è nota come legge di composizione degli spostamenti.
Detta invece vr la velocità di un punto in un sistema di riferimento e vt la velocità con cui si muove rispetto al primo un secondo sistema di riferimento, allora la velocità del punto misurata rispetto al secondo sistema sarà pari a:
v = vr + vt
Tale equazione è nota come legge di composizione delle velocità.
Legge di invarianza dell'accelerazione
Consideriamo due sistemi di riferimento inerziali, uno in moto con velocità costante rispetto all'altro.
Se un punto è soggetto ad una certa accelerazione nel primo sistema di riferimento, l'accelerazione misurata nel secondo sarà sempre la stessa:
a = ar
Così come l'accelerazione dunque anche le forze misurate in ambedue i sistemi saranno le medesime.
Esercizio #1
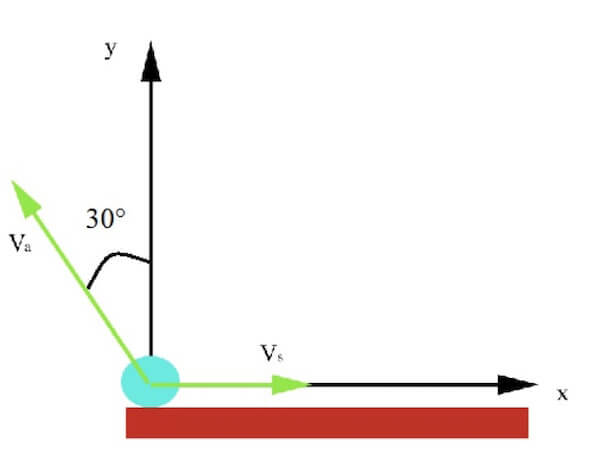
Una sfera posta sopra un'asta, si sta muovendo verso destra alla velocità costante di 3 m/s, mentre l'asta sta traslando, sempre a velocità costante ma di modulo 4 m/s, in una direzione che forma un angolo di 30° con la verticale.
Determinare l'equazione della traiettoria descritta dalla sfera derivante dalla composizione dei due moti rispetto ad un sistema di assi cartesiano Oxy con centro nella sfera.
Applicare poi le trasformazioni di Galileo per descrivere l'equazione della traiettoria in un sistema Ox'y' che si muove alla stessa velocita e nella stessa direzione dell'asta, coincidente con Oxy all'istante iniziale.
Lo svolgimento dell'esercizio lo trovi qui: esercizio sulle trasformazioni di galileo.
Esercizio #2
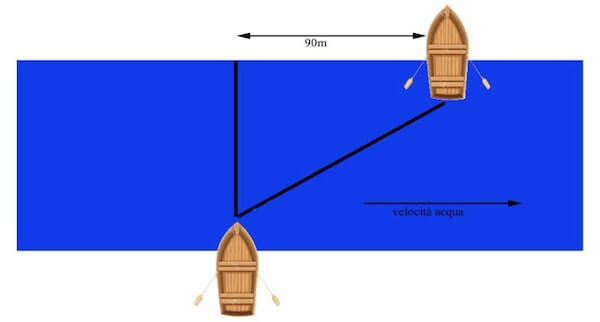
Una barca attraversa un fiume ad una velocità di 1 m/s rispetto alla corrente che invece scorre perpendicolarmente.
La barca impiega 3 minuti per raggiungere l'altra sponda, ma a causa della presenza dell'acqua in movimento, la posizione finale in cui si ritrova risulta traslata lateralmente di 90 m rispetto alla posizione di partenza.
Calcolare la larghezza del fiume, la velocità dell'acqua e la velocità tenuta dalla barca rispetto alle sponde.
Lo svolgimento dell'esercizio lo trovi qui: applicazione delle trasformazioni galileiane.
Link correlati:
Cosa afferma e su quali postulati si fonda la relatività ristretta?
dilatazione dei tempi, tempo proprio e tempo non proprio
Studia con noi