Esercizio sulle trasformazioni di galileo
Esercizio svolto sulle trasformazioni di galileo
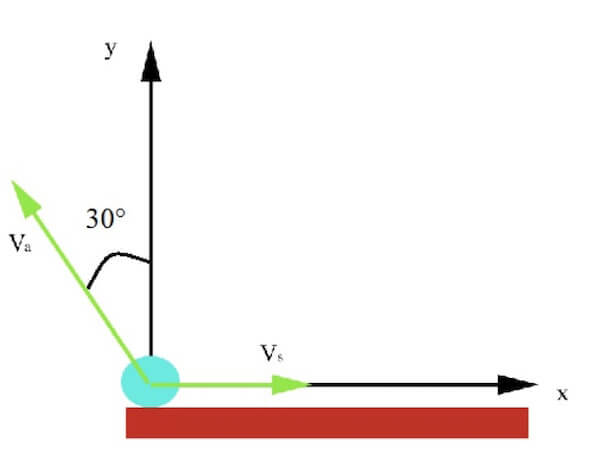
Una sfera posta sopra un'asta, si sta muovendo verso destra alla velocità costante di 3 m/s, mentre l'asta sta traslando, sempre a velocità costante ma di modulo 4 m/s, in una direzione che forma un angolo di 30° con la verticale.
Determinare l'equazione della traiettoria descritta dalla sfera derivante dalla composizione dei due moti rispetto ad un sistema di assi cartesiano Oxy con centro nella sfera.
Applicare poi le trasformazioni di Galileo per descrivere l'equazione della traiettoria in un sistema Ox'y' che si muove alla stessa velocità e nella stessa direzione dell'asta, coincidente con Oxy all'istante iniziale.
Svolgimento dell'esercizio
Per determinare la traiettoria della sfera dobbiamo procedere alla somma vettoriale delle due velocità che dà luogo ad una componente x e y della velocità risultante, e scriverne le relative equazioni orarie lungo i due assi.
Procediamo dunque alla somma vettoriale di:
Vrisultante = Va + Vs
Essendo in un piano bidimensionale, la precedente equazione vettoriale si traduce in due equazioni scalari, una lungo la direzione dell'asse x ed una lungo la direzione dell'asse y.
Per cui:
Vr,x = Vs – Va,x
Vr,y = Va,y
La componente x di Va è negativa, in quanto il vettore proiettato sull'asse x è rivolto verso sinistra.
La componente y di Vs è invece nulla in quanto il vettore giace sull'asse x.
Calcoliamo le componenti dei due vettori:
Va,x = Va ∙ sen30 = 4 ∙ ½ = 2 m/s
Va,y = Va ∙ cos30 = 4 ∙ √3/2 = 2 ∙ √3 m/s
Dunque:
Vr,x = Vs – Va,x = (3 – 2) m/s = 1 m/s
Vr,y = Va,y = 2 ∙ √3 m/s
Le due componenti della velocità risultante danno vita a due moti rettilinei uniformi lungo i due assi di equazione oraria (vedi: moto rettilineo uniforme):
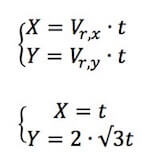
Sostituendo la prima nella seconda otteniamo:
Y = 2 ∙ √3 ∙ X
che rappresenta l'equazione della traiettoria della sfera nel sistema di riferimento Oxy.
Poniamoci adesso nel sistema di riferimento Ox'y', che si muove a velocità costante rispetto al primo e dunque rappresenta un sistema di riferimento inerziale.
La velocità V di tale sistema di riferimento coincide sia in modulo sia nella direzione con quella dell'asta e dunque:
V = Va
Per le trasformazioni di Galileo le nuove coordinate saranno:
x' = x - V∙t
y' = y - V∙t
in cui il tempo t' risulta uguale ed invariante rispetto al tempo t misurato nel primo sistema di riferimento.
Allora:
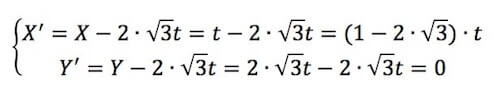
Dunque la nuova traiettoria nel sistema di riferimento Ox'y' sarà descritta da:
Y' = 0
Studia con noi