Numero di fenditure di un reticolo
Calcolo del numero di fenditure di un reticolo di diffrazione
Un reticolo largo 2 cm viene illuminato con luce di lunghezza d'onda pari a 600 nm.
Sapendo che si rileva una deviazione di θ = 30° nello spettro del secondo ordine, determinare da quante fenditure è composto il reticolo.
Svolgimento dell'esercizio
Per risolvere il problema iniziamo anzitutto a raccogliere i dati:
λ = 600 nm = 600 ∙ 10-9 m = 6 ∙ 10-7 m
θ = 30°
L = 2 cm = 2 ∙ 10-2 m
m = 2 (secondo ordine)
L'equazione che descrive la distribuzione delle frange dei massimi prodotta da un reticolo di diffrazione è:
senθ = m · λ / d
In cui:
- θ è l'angolo formato dalla direzione del raggio diffratto rispetto alla normale al piano del reticolo;
- m è l'ordine dei massimi;
- λ è la lunghezza d'onda della radiazione incidente utilizzata;
- d è il passo del reticolo.
La larghezza complessiva del reticolo considerando le N fenditure è pari a:
L = N ∙ d
per cui l'incognita che dobbiamo ricavare N è pari a:
N = L / d
Considerando l'equazione del reticolo:
senθ = m · λ / d
Ricaviamo d:
d = m · λ / senθ
Allora avremo:
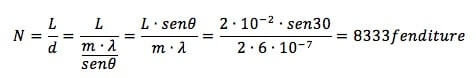
Link correlati:
esercizio sul reticolo di diffrazione
Studia con noi