Velocità di propagazione di un'onda trasversale
Calcolo della velocità di propagazione di un'onda trasversale
La corda di un violino è composta di un materiale che possiede densità lineare di 2,5 g/m ed è sottoposta ad una tensione di 10 N.
Determinare la velocità dell'onda che si propaga lungo la corda e la frequenza sapendo che la lunghezza d'onda vale 14,4 cm.
Svolgimento dell'esercizio
L'esercizio propone il caso di una corda di violino che è sottoposta ad una tensione di 10 Newton e possiede una densità lineare di 2,5 g/m.
Si vuole determinare la velocità di propagazione e la frequenza dell'onda sapendo che la lunghezza d'onda vale 14,4 cm.
Sappiamo che la velocità di propagazione di un'onda trasversale lungo una corda tesa vale:
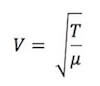
in cui T è la tensione a cui è sottoposta la corda e μ la sua densità lineare.
La tensione T vale 10 N mentre la densità lineare deve essere espressa in unità del Sistema Internazionale, ovvero in kg/m:
μ = 2,5 g/m = 2,5∙10-3 kg/m
Per cui:
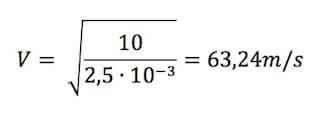
Infine per ricavare la frequenza dell'onda utilizziamo la relazione:
V = λ ∙ f
in cui la lunghezza d'onda λ va espressa in m:
f = V/ λ = 63,24/(14,4∙10-2) = 439,2 Hz
Prova tu
La velocità di propagazione di un'onda trasversale lungo una corda tesa è di 30 m/s.
Sapendo che la tensione a cui è sottoposta la corda è di 90 N, determinare la densità lineare della corda.
Determinare infine la lunghezza d'onda della sapendo che la frequenza dell'onda è di 150 Hz.
Lo svolgimento dell'esercizio lo trovi qui: calcolo della densità lineare di una corda.
Studia con noi