Legge di Biot-Savart

Cosa afferma la legge di Biot-Savart?

Così come le cariche elettriche sono le sorgenti dei campi elettrostatici quando sono in quiete, esse divengono sorgenti del campo magnetico quando sono poste in moto nelle correnti elettriche. Dunque un filo percorso da corrente diventa come un magnete una sorgente di campo magnetico.

Ci poniamo adesso il problema del calcolo del campo magnetico generato da un filo rettilineo percorso da corrente.

Direzione e verso del campo magnetico generato da un filo

Consideriamo un filo conduttore rettilineo molto lungo percorso da una corrente di intensità i.

Dall'esperienza di Oersted sappiamo che questo filo genera attorno a se un campo magnetico le cui linee sono circonferenze concentriche al filo per cui la corrente che scorre nel conduttore si dice concatenata al percorso delle linee del campo magnetico cioè si trova all'interno della porzione di piano racchiuso dalla linea stessa di campo magnetico che come ricordiamo sarà sempre chiusa. Per cui la direzione del campo magnetico generato da un filo rettilineo percorso da corrente è una circonferenza concentrica al filo.

Tale proprietà è evidenziabile spargendo della limatura di ferro attorno al filo: in assenza di corrente la limatura risulta posta in maniera disordinata attorno al filo. Nel momento in cui si fa circolare la corrente nel filo invece i pezzettini di ferro di dispongono proprio su linee di circonferenze concentriche al filo.

Per determinare invece il verso si può utilizzare la regola della mano destra in cui il pollice segue il verso della corrente e le dita restituiscono il verso con cui le linee circondano la corrente.

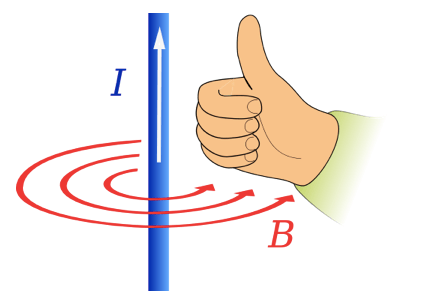
Verso del campo magnetico

Intensità del campo magnetico generato da un filo rettilineo

Per determinare l'intensità del campo magnetico generato da un filo rettilineo percorso da corrente ci avvaliamo del teorema della circuitazione di Ampere. Che cosa è la circuitazione di un campo vettoriale?

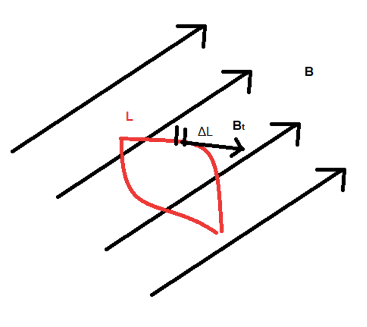
Consideriamo come campo vettoriale un campo magnetico uniforme (linee di campo parallele) B e al suo interno un percorso chiuso, cioè una linea di lunghezza L, di cui stabiliamo arbitrariamente un verso di percorrenza positivo.

Suddividiamo il filo in tanti pezzettini di lunghezza ΔL e consideriamo la componente tangente B_t del campo magnetico a tale pezzettino di percorso ovvero la proiezione del campo in quell'elementino di percorso dato dal prodotto tra l'intensità del campo magnetico B e il coseno dell'angolo tra campo e pezzettino di filo.

La somma di tutti i prodotti tra la componente tangente del campo magnetico alla generica suddivisione del percorso per la lunghezza della suddivisione stessa rappresenta la circuitazione del campo B lungo la linea L.

circuitazione del campo B

Detti cioè B_t1 e ΔL₁, B_t2 e ΔL₂, …… fino a B_ti e ΔL_i la circuitazione di B sulla linea di lunghezza L è data da:

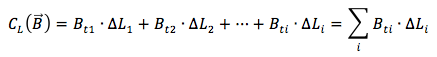
circuitazione di B sulla linea di lunghezza L

Il teorema di Ampere afferma che la circuitazione del campo magnetico lungo la linea L è pari al prodotto della permeabilità magnetica nel vuoto μ₀ per la somma algebrica delle correnti concatenate alla linea L, cioè soltanto quelle correnti che attraversano la superficie racchiusa da L:

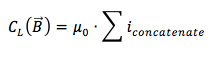
Formula del teorema di Ampere

Ora riprendiamo il nostro filo rettilineo percorso da corrente i di cui vogliamo calcolare l'intensità del campo generato e scegliamo come linea chiusa una circonferenza di raggio d che quindi rappresenterà la distanza dal filo.

Sappiamo che il campo magnetico sarà tangente in ogni punto della circonferenza L:

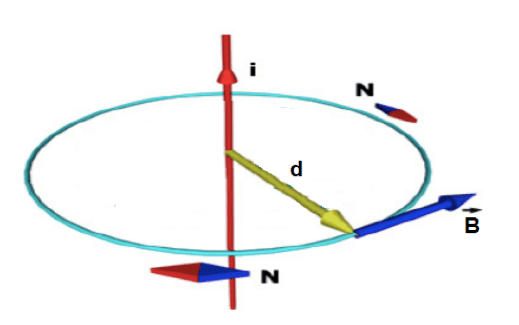
Campo magnetico tangente

Applichiamo dunque il teorema della circuitazione di Ampere alla nostra circonferenza che avrà lunghezza 2∙π∙d:

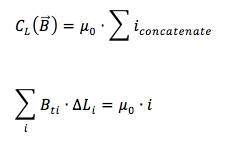
Applichiamo dunque il teorema della circuitazione di Ampere

Il campo magnetico B è costante ovvero assume lo stesso valore per tutti i punti posti lungo la circonferenza e l'unica corrente concatenata al percorso è la corrente i che scorre nel filo per cui:

B ∙ 2 ∙ π ∙ d = μ₀ ∙ i

che riscritta come:

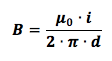
Legge di Biot Savart

rappresenta la legge di Biot-Savart la quale afferma che il campo magnetico generato da un filo rettilineo percorso da corrente dipende in maniera inversamente proporzionale dalla distanza d a cui si ci pone dal filo e in maniera direttamente proporzionale dalla corrente che scorre in esso.

Link correlati: