Campo magnetico di due fili paralleli percorsi da corrente
Calcolo del campo magnetico di due fili paralleli percorsi da corrente
Due fili conduttori rettilinei molto lunghi posti a distanza 2a = 4 cm tra di loro sono percorsi da due correnti aventi la stessa intensità di 50 A ma con versi opposti come in figura.
Calcolare il modulo del campo magnetico risultante sull'asse mediano perpendicolare tra i due fili in funzione della generica quota z dell'asse verticale.
Svolgimento dell'esercizio
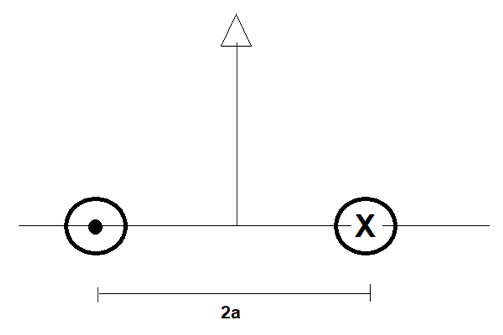
Le due correnti di sinistra e di destra sono rispettivamente uscente dal foglio ed entrante nel foglio.
Applicando la regola della mano destra su un generico punto dell'asse indicato in figura avremo che i campi generati dai due fili saranno orientati come nella seguente figura e avranno stessa intensità in quanto le correnti sono uguali in modulo e identica è la distanza d da ognuno dei due fili:
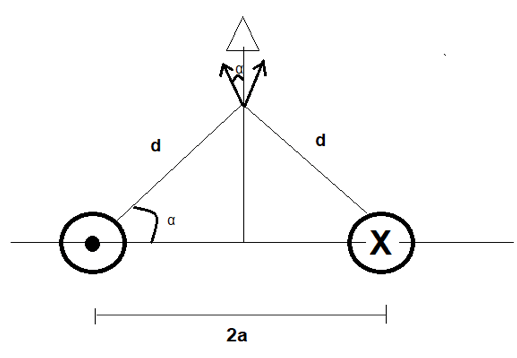
Ogni vettore campo magnetico disegnato nel generico punto dell'asse ha una componente orizzontale ed una verticale cioè una proiezione orizzontale ed una verticale.
Le due proiezioni orizzontali dei due vettori sono uguali ed opposte quindi si annullano.
Le due direzioni verticali invece si sommano restituendo la risultante complessiva.
Gli angoli che i due vettori formano con l'asse sono i medesimi e detto α ognuno di essi avremo che ogni componente verticale sarà pari a:
Bv = B∙ cos α
Ricordando che d rappresenta il raggio della circonferenza a cui il vettore B disegnato è tangente, risulterà che il vettore B è perpendicolare al raggio e per costruzione l'angolo α da esso formato con l'asse verticale è lo stesso che la distanza d forma con l'asse orizzontale.
Per ricavare il valore del coseno di questo angolo considerando che ogni filo dista a dall'origine a cm:
d∙ cos α = a
in cui z l'ordinata del punto in cui sono disegnati i due vettori campo magnetico.
Dalla precedente risulta che:
cosα = a / d
Per cui il campo magnetico nel punto dell'asse verticale vale:
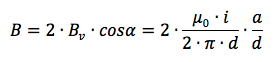
Applichiamo il teorema di Pitagora al triangolo rettangolo di ipotenusa d per ricavare quest'ultima in funzione di a e di z:
![]()
Per cui otteniamo:
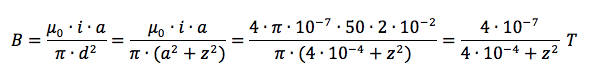
Pertanto abbiamo calcolato il valore del modulo del campo magnetico risultante sull'asse mediano perpendicolare tra i due fili in funzione della generica quota z dell'asse verticale.
Link correlati:
Quali sono le differenze tra il campo magnetico e il campo elettrico?
Esercizio svolto e commentato sulla esperienza di Faraday
Che cos'è la riluttanza?
Calcolo del valore del campo magnetico al centro di un quadrato
Studia con noi