Forza magnetica su un filo percorso da corrente
Quanto vale la forza magnetica su un filo percorso da corrente?
Consideriamo un filo conduttore percorso da corrente e posto in una regione dello spazio in cui è presente un campo magnetico.
Su ogni carica in movimento agisce la forza di Lorentz in quanto si tratta di cariche in movimento in un campo magnetico. La somma di tutte le forze di Lorentz agenti su ciascuna carica avrà come risultante una forza magnetica che si osserva macroscopicamente agire sul filo.
L'espressione della forza totale agente sul conduttore è la seguente (per maggiori info su come si è arrivati a questa formula si veda: esperimento di Faraday):
![]()
in cui (in grassetto vengono rappresentate le grandezze vettoriali):
- L è un vettore che ha la direzione e la lunghezza del filo rettilineo e il verso della corrente i;
- B è il vettore campo magnetico;
- i è l'intensità della corrente.
In modulo di tale forza è:
F = i ∙ B ∙ L ∙ senα
in cui α è l'angolo compreso tra i vettori B e L. La forza magnetica risulta dunque massima quando il filo è perpendicolare al campo magnetico (α = 90°) mentre è nulla quando il filo è parallelo al campo magnetico (α = 0°).
Per stabilire direzione e verso della forza magnetica agente sul filo conduttore percorso da corrente è necessario invece applicare la regola della mano destra.
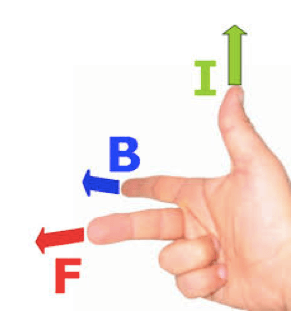
Applichiamo in due esercizi quanto detto fino ad ora.
Esercizio #1
Un'asta conduttrice ha massa pari a 15 g ed una lunghezza di 20 cm. Essa è posta tra due guide verticali che le consentono di scorrere verso il basso a causa della forza peso ed immersa in una regione di spazio in cui è presente un campo magnetico uniforme B entrante nel piano nel quale scorre l'asta e di intensità pari a 0,74 T. Se l'asta si muove a velocità costante determinare la corrente che scorre in essa.
Svolgimento dell'esercizio
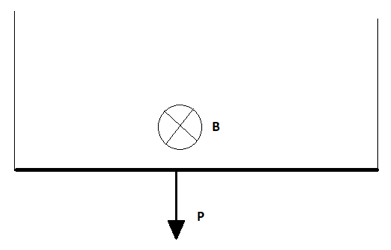
Se l'unica forza ad agire sull'asta fosse la forza peso allora essa si muoverebbe verso il basso con un'accelerazione. Invece poiché l'asta si muove di moto rettilineo uniforme a velocità costante vuol dire che l'accelerazione è nulla. Ciò significa che la risultante di tutte le forze agenti su di essa deve essere uguale a zero.
Le forze che agiscono sull'asta sono la forza Peso diretta vero il basso e necessariamente la forza magnetica che la controbilancia rivolta verso l'alto. Per ottenere tale verso della forza magnetica, ricordando la regola della mano destra, il verso della corrente dovrà necessariamente essere diretto verso destra.
Uguagliando forza peso e forza magnetica otteniamo:
m ∙ g = i ∙ L ∙ B
da cui possiamo ricavare l'intensità di corrente i:
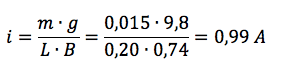
Esercizio #2
Una barretta conduttrice di lunghezza 45 cm e massa trascurabile, è sospesa tramite due molle metalliche di costante elastica K = 15 N/m, aventi lunghezza ad interruttore aperto pari a 25 cm e indeformabili in direzione perpendicolare alla loro lunghezza, ad un'asta rigida inserita all'interno di un circuito dotato di interruttore e di generatore di tensione da 12 V.
La resistenza totale del circuito è pari a 5,2 Ω e la parte centrale dell'asta rigida non è conduttrice. La barretta insieme alle due molle è immersa in un campo magnetico uniforme uscente dal piano di intensità pari a 380 mT.
Determinare: la corrente che scorre nel circuito quando viene chiuso l'interruttore, modulo direzione e verso delle forze magnetiche agenti su barretta e molle, la nuova condizione di equilibrio del circuito.
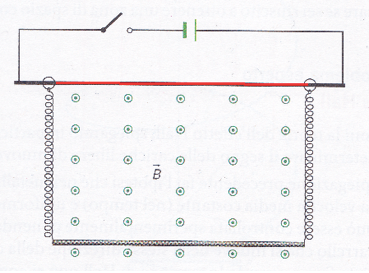
Svolgimento dell'esercizio
Una volta chiuso l'interruttore la corrente circola nelle parti disegnate in nero del circuito e attraverso le due molle con la barretta appesa ad esse. Per calcolare l'intensità di corrente elettrica che circola nel circuito utilizziamo la prima legge di Ohm:
i = V / R = 12 / 5,2 = 2,3 A
Per stabilire direzione e verso delle forze magnetiche agenti su molle e barretta dobbiamo prima stabilire il verso con cui scorre la corrente all'interno del circuito. Il verso reale della corrente elettrica è quello che va dal polo negativo al polo positivo.
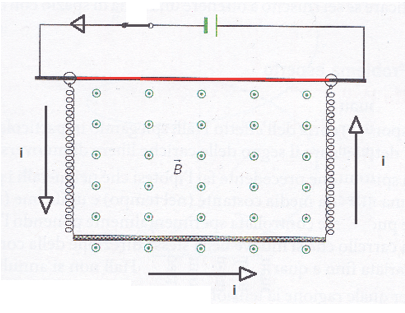
Dunque applicando la regola della mano destra ai tre elementi:

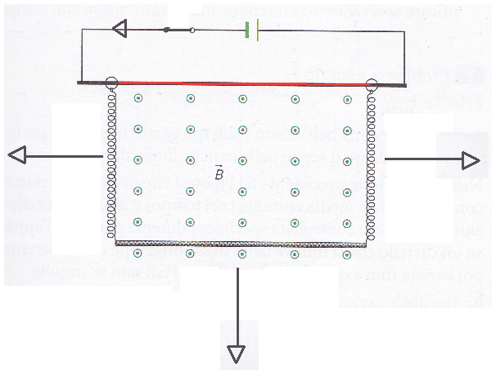
otteniamo direzione e verso delle forze magnetiche agenti su molle e barretta:
Per stabilirne l'intensità ricordiamo l'espressione della forza magnetica agente sul conduttore:
![]()
Cioè la forza magnetica agente su un filo percorso da corrente i, di lunghezza L ed immerso in un campo magnetico di intensità B è data dal prodotto vettoriale del vettore diretto lungo la direzione del filo nel verso della corrente ed il vettore campo magnetico moltiplicato per la corrente i.
In modulo quindi la forza magnetica è pari al prodotto dell'intensità di corrente elettrica i, per la lunghezza L del filo, per il modulo B del campo magnetico per il seno dell'angolo compreso tra filo e campo magnetico:
F = i ∙ B ∙ L ∙ senα
Gli angoli tra le direzioni delle molle e della barretta col quella del campo magnetico è sempre 90°.
Dunque sulle molle agirà una forza in modulo pari a:
Fmolle = i ∙ B ∙ Lmolla = 2,3 ∙ 0,380 ∙ 0,25 = 0,22 N
Mentre sulla barretta:
Fbarretta = i ∙ B ∙ Lbarretta = 2,3 ∙ 0,380 ∙ 0,45 = 0,39 N
Essendo le molle indeformabili lungo la direzione perpendicolare alla loro lunghezza, alla chiusura dell'interruttore si osserverà un allungamento verso il basso delle due molle a causa della comparsa della forza magnetica sulla barretta. All'equilibrio allora si avrà uguaglianza tra la forza elastica data dalla presenza delle due molle e la forza magnetica:
Felastica = Fmagnetica
Ricordando che il modulo della forza elastica per una molla è il prodotto della costante elastica per l'allungamento e che due molle collegate in parallelo come nel nostro caso equivalgono ad una sola molla con costante elastica data dalla somma delle due costanti elastiche, avremo:
(K + K) ∙ ∆x = i ∙ Lbarretta ∙ B
Da cui:
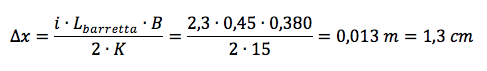
Dunque nella nuova configurazione il circuito si sarà allungato verso il basso di 1,3 cm.
Link correlati:
Quali sono le differenze tra il campo magnetico e il campo elettrico?
Che cosa è la permeabilità magnetica?
Studia con noi