Circuitazione del campo elettrico
Che cos'è la circuitazione del campo elettrico?
In questa lezione vedremo che cos'è la circuitazione del campo elettrico, come la si calcola e qual è una importante conclusione del risultato della circuitazione del campo elettrico. Si tenga presente che, nel testo dell'articolo, le grandezze vettoriali vengono rappresentate in grassetto.
Consideriamo un campo elettrostatico E cioè generato da cariche elettriche che sono ferme) ed una linea chiusa orientata L (orientata vuol dire che bisogna stabilire il verso di percorrenza di questa linea circuitale).
Immaginiamo di dividere la linea L in un numero n molto elevato di piccoli tratti ognuno di lunghezza Δl1, Δl2, Δl3…. Δln in modo da poter considerare il campo elettrico uniforme E1, E2, E3, ... , En per ogni tratto infinitesimo.
Associamo ad ogni tratto Δl il relativo vettore spostamento Δl1, Δl2, .... , Δln associato al movimento lungo la linea orientata.
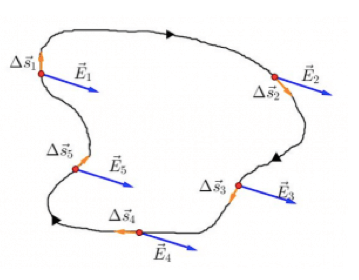
Si definisce circuitazione di E lunga la linea L la somma di tutti i prodotti scalari tra ogni vettore campo elettrico misurato nell'i-esima parte in cui è stata suddivisa la linea e il relativo vettore spostamento:
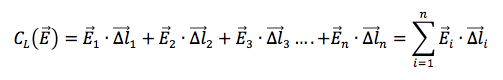
Ricordiamo che il prodotto scalare di due vettori è una grandezza scalare cioè un valore pari al prodotto del modulo dei due vettori per il coseno dell'angolo tra essi compreso.
L'unità di misura della circuitazione è il Volt [V] in quanto il prodotto di un campo elettrico per una lunghezza restituisce proprio la differenza di potenziale elettrico che si misura in volt.
Quanto vale la circuitazione del campo elettrostatico
Consideriamo una carica di prova q che percorre la linea chiusa orientata L immersa in un campo elettrostatico E. Per ogni tratto infinitesimo i-esimo in cui si suddivide la linea L, la carica q subisce la forza elettrica pari al prodotto della carica per il valore del campo elettrico in quel tratto:
Fi = q ∙ Ei
Il lavoro W svolto dalla forza elettrico lungo lo spostamento i-esimo Δli è pari al prodotto scalare tra la forza i-esima e lo spostamento stesso:
Wi = Fi ∙ Δli
Ricordando che la differenza di potenziale ΔV tra due punti è pari al rapporto cambiato di segno tra il lavoro svolto dalla forza elettrica per spostare la carica tra quei due punti e la carica stessa, avremo che la d.d.p. tra i due punti estremo dello spostamento i-esimo vale:
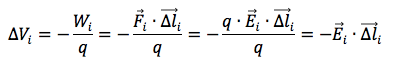
Per cui:
Ei ∙ Δli = - ΔVi
Allora la circuitazione C del campo elettrico E lungo la linea orientata chiusa L può essere riscritta come:
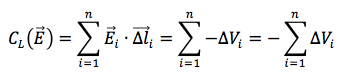
Ora il potenziale nel tratto iniziale del primo spostamento i = 1 varrà V0 mentre quello nel tratto finale dello stesso spostamento varrà V1. All'inizio del secondo spostamento il potenziale varrà ancora V1 mentre nel tratto finale V2. E così via….
Allora la sommatoria delle differenze di potenziale presenti tra l'inizio e la fine può essere sviluppata come:
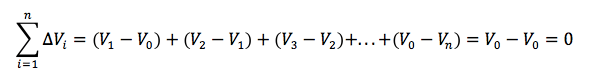
Infatti partendo dal punto iniziale si torna sempre al punto iniziale perché la linea è chiusa. In questo punto iniziale il potenziale vale V0. Abbiamo dimostrato allora che per un campo elettrostatico la circuitazione vale zero ovvero è nulla:
![]()
Il significato fisico di questa equazione matematica è che il campo elettrostatico è un campo conservativo, ovvero il lavoro svolto dalle forze del campo non dipende dal cammino percorso ma soltanto dalla posizione iniziale e da quella finale.
Una conseguenza del risultato della circuitazione del campo elettrico
Una importante conseguenza del fatto che il campo elettrico sia conservativo e che la sua circuitazione lungo una linea chiusa dunque vale zero porta all'enunciato del teorema delle maglie o seconda legge di Kirchhoff che afferma: la somma algebrica delle differenze di potenziale lungo una maglia (percorso circuitale chiuso) è uguale a zero.
Esercizio
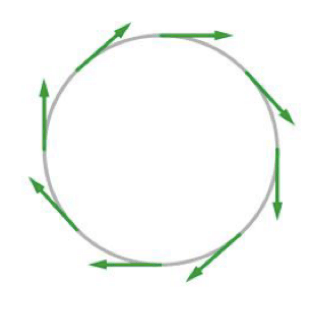
Un campo elettrico è rappresentato da linee di campo circolari. Il vettore campo elettrico dunque risulta tangente in ogni punto a tali linee come nella linee rappresentata in figura.
Sapendo che il modulo del campo elettrico è costante è vale 150 V/m ed il raggio della linea chiusa è di 4 cm determinare la circuitazione lungo tale linea. Si tratta di un campo conservativo?
Svolgimento dell'esercizio
Immaginando di suddividere la circonferenza lungo la quale calcolare la circuitazione del campo in moltissimi tratti di lunghezza infinitesima Δl, si definisce circuitazione di E lunga la linea L la somma di tutti i prodotti scalari tra ogni vettore campo elettrico misurato nell'i-esima parte in cui è stata suddivisa la linea e il relativo vettore spostamento:
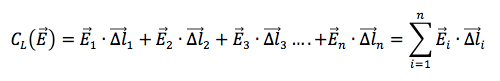
Essendo il campo elettrico però costante avremo che:
E1 = E2 = …. = En = 150 V/m
E sommando tutti i tratti di lunghezza Δl si ottiene la circonferenza di lunghezza 2∙π∙r. Dunque la circuitazione di questo campo lungo la linea vale:
C(E) = E∙2∙π∙r = 150 ∙2 ∙π ∙ 0,04 = 37,7 V
Essendo la circuitazione del campo non nulla, si tratta di un campo non conservativo, quindi non può essere un campo elettrostatico. Inoltre le linee di forza di un campo conservativo sono aperte, mentre quelle di un campo non conservativo sono chiuse.
Link correlati:
Esercizi svolti e commentati di elettrostatica
Esercizio sul calcolo della circuitazione del campo elettrico
Quali sono le differenze tra il campo magnetico e il campo elettrico?
Che cos'è la circuitazione del campo magnetico?
Che cos'è il pozzo di Faraday?
Studia con noi