Prodotto scalare
Come si esegue un prodotto scalare?
Dati due vettori 
e 
si definisce l'operazione di prodotto scalare tra essi 
:
= a · b · cos α
in cui a e b sono i moduli dei due vettori mentre α è l'angolo tra essi compreso:
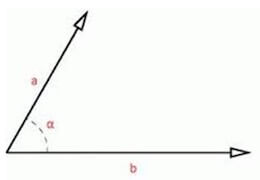
Il risultato del prodotto scalare è un numero ovvero una grandezza di tipo scalare determinata solo dal valore numerico.
Essendo la funzione coseno compresa tra -1 e 1 il valore che può assumere il risultato di può variare da un minimo di (- a · b) ad un massimo di (a · b).
Il primo caso si ha quando l'angolo tra i due vettori vale 180 °, ovvero quando i due vettori sono posti lungo la stessa direzione ma rivolti con versi opposti.
Il secondo caso invece si ha quando i vettori sono equiversi e sono sempre giacenti lungo la stessa retta.
Se si verifica che i due vettori sono perpendicolari tra di loro (angolo di 90°) allora il prodotto scalare vale zero.
Riassumiamo quindi i tre casi nel seguente schema:
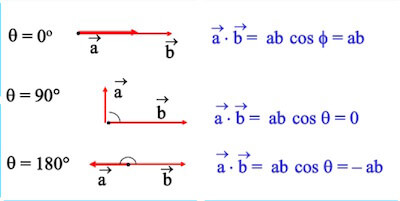
Conoscendo il valore del prodotto scalare è possibile ricavare il coseno dell'angolo tra essi compreso:
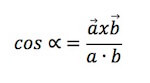
e tramite la funzione arcoseno si può quindi calcolare proprio il valore dell'angolo espresso in gradi o in radianti.
Significato geometrico del prodotto scalare
Il prodotto scalare è strettamente connesso al significato di proiezione ortogonale.
Eseguire il prodotto scalare tra i due vettori 
e 
vuol dire infatti calcolare il prodotto tra il modulo del vettore e la componente del vettore lungo la direzione di , ovvero per la misura della proiezione del secondo vettore lungo il primo:
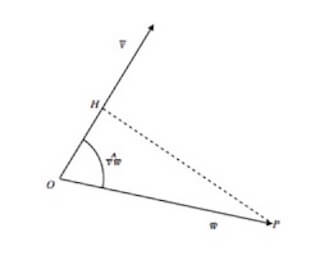
Nella figura il prodotto scalare tra i due vettori è quindi il prodotto di v per il segmento OH il quale è appunto calcolabile come w · cos α , con α angolo compreso tra i due vettori 
.
Proprietà del prodotto scalare
Dati i vettori a, b e c e sia λ un numero reale, le proprietà del prodotto scalare sono le seguenti:
Proprietà commutativa:
a x b = b x a
Omogeneità:
(λ · a) x b = λ · (a x b)
a x (λ · b) = λ · (a x b)
Proprietà distributiva:
(a + b) x c = a x c + b x c
Elemento nullo:
il prodotto scalare è nullo solo se i due vettori sono perpendicolari.
Calcolo del prodotto scalare attraverso le componenti
Dati i due vettori e appartenenti al piano bidimensionale R2 e quindi dotati entrambi di due componenti:
= (ax ; ay)
= (bx ; by)
Il prodotto scalare è pari a:
= (ax · bx + ay · by)
Esercizio sul prodotto scalare
Dati i vettori nel piano a = (2;1) e b = (1;3) calcolare il prodotto scalare tra i due vettori e l'angolo tra essi formato.
Lo svolgimento lo trovi qui: esercizio sul prodotto scalare.
Link correlati:
Come si esegue la differenza tra due vettori?
Studia con noi