Numero di spire e lunghezza di un solenoide
Esercizio sul calcolo del numero di spire e lunghezza di un solenoide
Si vuole costruire un solenoide in cui il campo magnetico interno ha intensità pari a 45 μT .
Si ha disposizione del filo di rame (ρ = 1,69 ∙ 10-8 Ω∙m) di diametro pari a 0,300 mm di lunghezza totale pari a 50,0 m da avvolgere attorno ad un cilindro isolante di diametro 3,60 cm.
Determinare il numero di spire da realizzare attraverso l'avvolgimento del filo attorno al cilindro sfruttando tutta la lunghezza del filo stesso, la lunghezza del solenoide finale, la tensione da applicare ai capi del solenoide per ottenere il valore di campo magnetico desiderato.
Svolgimento dell'esercizio
Un solenoide è un avvolgimento di N spire, di lunghezza L che se percorso da corrente i crea al suo interno un campo magnetico B di intensità pari a:
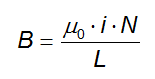
Dai dati forniti dal problema sappiamo solo che:
B = 45 μT = 4,5 ∙ 10-5 T
Per determinare il numero di avvolgimenti N che si possono realizzare col filo a disposizione dividiamo la lunghezza totale l del filo per la circonferenza C del cilindro isolante (di cui conosciamo il diametro D) in modo da ricavare quanti giri si possono effettuare attorno al cilindro sfruttando l'intera lunghezza l del filo di rame.
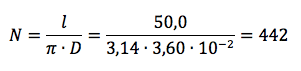
La lunghezza L del solenoide che si ottiene cosi non è altro che il prodotto del numero di spire N per il diametro d di ogni spira:
L = N∙ d = 442∙ 0,300 ∙ 10-3 = 0,13 m
Possiamo così ricavare l'intensità di corrente elettrica i che deve scorrere nel solenoide per ottenere il campo B al suo interno. Dalla formula:
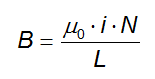
ricaviamo i:

La tensione da applicare ai capi del solenoide per avere un'intensità di corrente pari a i è data dalla prima legge di Ohm:
V = R ∙ i
in cui R è la resistenza del solenoide calcolabile a partire dalla seconda legge di Ohm:
R = ρ · L / S
in cui l è la lunghezza del filo ed S la sua sezione (calcolabile come prodotto di π per la metà del diametro del filo fornito al quadrato, cioè il raggio del filo):
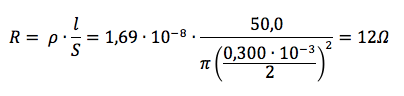
Allora la tensione V da applicare vale:
V = R ∙ i = 12 ∙ 0,01 = 0,12 V
Link correlati:
Calcolo del valore del campo magnetico al centro di due spire
Calcolo del flusso del campo magnetico attraverso una bobina
Esercizio su un fascio di protoni che deve essere curvato di 90°
Quanto vale il campo magnetico di una spira circolare?
Calcolo della coefficiente di autoinduzione di un solenoide
Studia con noi