Campo magnetico di una spira
Quanto vale il campo magnetico di una spira circolare?
Consideriamo un filo conduttore avvolto ad anello a formare un percorso circolare cioè chiuso. Tale configurazione prende il nome di spira circolare. Le spire possono avere le più svariate forme quadrate, rettangolari … qui per semplicità tratteremo soltanto le spire circolari.
Quando una spira è percorsa da una corrente i essa si comporta proprio come un magnete generando attorno a sé un campo magnetico le cui linee di campo attraversano la superficie del piano che contiene la spira stessa. In particolare sull'asse della spira (cioè la retta perpendicolare al piano della spira che passa per il suo centro) il campo magnetico B risulta perpendicolare al piano stesso che contiene la spira.
Per determinare il verso del campo magnetico generato da una spira si utilizza la regola della mano destra in cui le dita seguono il verso con cui scorre la corrente e il pollice indicherà dunque il verso del campo magnetico:
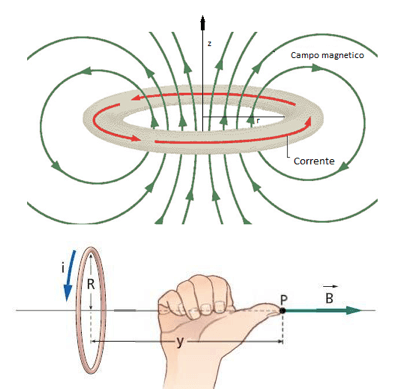
La parte di piano in cui le linee di campo entrano nel piano della spira costituirà il polo Sud della spira mentre la parte di piano da cui esse fuoriescono sarà il polo Nord.
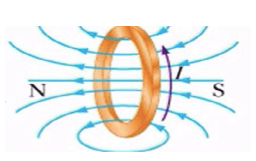
Intensità del campo magnetico al centro e sull'asse
Quanto vale in modulo il campo magnetico generato dalla spira? Concentriamoci sul valore del campo magnetico nel centro della spira circolare. Dunque consideriamo una spira circolare di raggio R e percorsa da intensità di corrente pari a i.
Suddividiamo la spira in tanti pezzettini infinitesimi di lunghezza ΔL e calcoliamo il valore del campo magnetico generato da ogni pezzettino nel centro della spira:
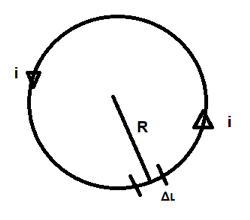
Per la regola della mano destra il tratto ΔL di filo percorso di corrente, considerato come rettilineo visto che è molto piccolo, genererà un campo magnetico al centro della spira che sarà uscente dal foglio (vedi esperienza di Oersted, pollice orientato come i e dita indicano direzione e verso di B al centro). Il tratto ΔL genererà al centro della spira un campo magnetico di intensità ΔB pari a:
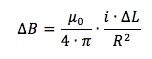
in cui μ0 è la permeabilità magnetica nel vuoto e vale 4∙π∙10-7 N/A2.
La legge con cui si calcola ΔB è detta legge di Ampere - Laplace. Il campo B totale nel centro non è altro che la somma di tutti i contributi ΔB relativi a tutti i pezzettini ΔL in cui è stata suddivisa la circonferenza. E ricordando che la lunghezza di una circonferenza è pari a 2 ∙π∙ R ponendo uguale tale prodotto alla somma di tutti i ΔL otteniamo:
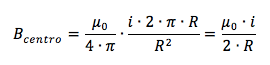
Dunque la spira è sorgente di campo magnetico e tale campo magnetico al centro del piano contenente la spira risulta direttamente proporzionale alla corrente che circola nella spira ed inversamente proporzionale al suo raggio.
Come si calcola il campo magnetico risultante su un punto posto sull'asse della spira?
Partiamo sempre dalla configurazione in cui suddividiamo la lunghezza della spira in tanti pezzettini di lunghezza ΔL e consideriamo un punto P posto sull'asse della spira a distanza x dal centro e distanza a da ogni punto della linea della spira:
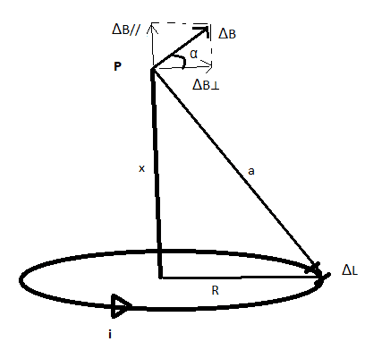
Ogni pezzettino ΔL genera un campo di intensità ΔB orientato secondo la regola della mano destra in maniera da risultare perpendicolare contemporaneamente al vettore tangente alla circonferenza in ΔL e al vettore costruito lungo la direzione del raggio. Tale campo ΔB avrà dunque due componenti una parallela (adagiata sull'asse)) e perpendicolare (che invece è ortogonale all'asse).
Quando andiamo a sommare tutti i contributi di campo magnetico generati da ogni pezzettino ΔL tutte le componenti ortogonali di B si elidono tra di loro e rimane solo il contributo di campo magnetico adagiato sull'asse della spira (così come era stato detto all'inizio di questo paragrafo).
La componente parallela di B si calcola detto α l'angolo che il vettore ΔB forma con l'asse x:
∆B// = ∆B ∙ senα
Ma per costruzione geometrica l'angolo tra il segmento a e l'asse vale anche esso α:
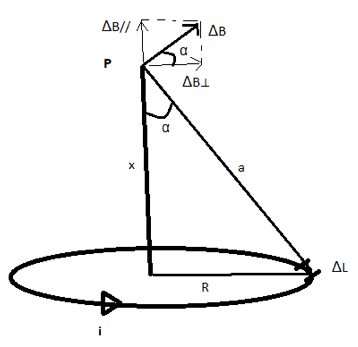
Per cui dalle regole trigonometriche applicate al triangolo rettangolo di lati a, x ed R si ha:
a ∙ senα = R
Da cui:
senα = R / a
E quindi la componente parallela di ΔB vale:
∆B// = ∆B ∙ senα = ∆B ∙ R / a
Ricordando per la legge di Ampere – Laplace che:
Sommando tutti i contributi ΔL otteniamo l'intensità B totale:
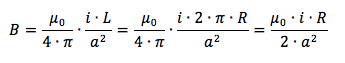
a è esprimibile come ipotenusa del triangolo rettangolo di lati a, x ed R, per cui per il teorema di Pitagora:
a2 = x2 + R2
Quindi:
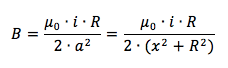
E in definitiva il campo totale nel punto P vale la somma di tutte le componenti parallele di B:
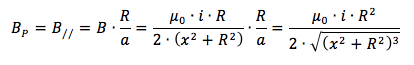
Nella precedente formula si è espresso ancora a utilizzando il teorema di Pitagora e si è portato sotto radice la somma di x2 + R2.
Per cui ricapitolando il campo magnetico al centro e nell'asse della spira si calcolano come:
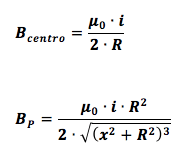
La prima formula (campo al centro della spira) discende direttamente dalla seconda quando la distanza dal centro è zero (x = 0).
Link correlati:
Quanto vale l'intensità del campo magnetico?
Che cos'è la densità di corrente elettrica?
Esercizio svolto sul selettore di velocità
Che cos'è il campo elettrico indotto?
Che cosa è la permeabilità magnetica?
Studia con noi