Calcolo del diametro di un conduttore
Prima legge di Ohm e calcolo del diametro di un conduttore
Un conduttore di alluminio ha sezione quadrata con lato di 5,0 mm ed è lungo 2,0 metri.
Calcolare la resistenza tra gli estremi.
Quale deve essere il diametro di un filo di rame lungo 1,0 metro a sezione circolare se la sua resistenza è la medesima di quella dell'alluminio?
Si sappia che:
ρrame = 1,7 · 10-8 Ω · m
ρalluminio = 2,8 · 10-8 Ω · m
Svolgimento
La seconda legge di Ohm fornisce la formula per il calcolo della resistenza di un conduttore metallico in funzione delle sue caratteristiche fisiche.
Infatti la resistenza è una caratteristica propria del conduttore e dipende dalla lunghezza L del conduttore, dalla sua sezione S e dal coefficiente di resistività secondo la formula:
R = ρ · L/S
I dati che ci fornisce il problema sono relativi a due conduttori.
Il primo conduttore è di alluminio ed ha la forma di un prisma quadrangolare, mentre il secondo conduttore è un filo di rame a forma cilindrica.
Chiamando 1 il primo conduttore e 2 il secondo abbiamo che:
l = 5,0 mm = 5,0 · 10-3 m lato di base del primo conduttore a forma di prisma
L1 = 2,0 m
ρ1 = 2,8 · 10-8 Ω · m
L2 = 1,0 m
ρ2 = 1,7 · 10-8 Ω · m
La resistenza del primo conduttore vale dunque:
R1 = ρ1 · L1/S1 = 2,8 · 10-8 · 2,0 / (5,0 · 10-3)2 = 2,24 · 10-3 Ω
Per cui la resistenza agli estremi del primo conduttore vale 2,24 m Ω.
Ora dal testo del problema si deduce che le resistenze dei due conduttori sono le medesime:
R1 = R2
Dunque poiché
R2 = ρ2 · L2/S2
ricaviamo la sezione dalla formula inversa:
S2 = ρ2 · L2/ R2 = ρ2 · L2/ R1 = 1,7 · 10-8 · 1 / 2,24 · 10-3 = 0,76 · 10-5 m2
Poiché il conduttore ha la sezione circolare, ricordando che l'area di un cerchio si calcola come:
S = π · R2
in cui R è il raggio, questo risulta pari a:
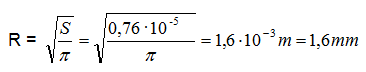
Essendo il diametro il doppio del raggio, si ha che:
d = 2 · R = 2 · 1,6 · 10-3 = 3,2 · 10-3 m = 3,2 mm
Dunque il diametro del conduttore in questione è di 3,2 mm.
Link correlati:
Qual è l'unità di misura della resistività?
Come si applica la formula della seconda legge di Ohm
Esercizio con applicazione della seconda legge di Ohm
Esercizio svolto e commentato sul coefficiente di variazione della resistività
Quali sono le formule inverse della seconda legge di Ohm?
Studia con noi