Campo elettrico in un condensatore
Campo elettrico tra le armature di un condensatore
Un condensatore piano, le cui armature hanno una superficie di 100 cm2 e sono distanti 0,5 cm, è posto all'interno di un circuito di lato 20 cm che sta attraversando una regione dello spazio sede di un campo magnetico perpendicolare al piano del circuito con velocità di 2 m/s.
Sapendo che l'intensità del campo è 0,5 T, calcolare il campo elettrico tra le armature del condensatore e la carica q che si deposita sulle armature.
Svolgimento
Il circuito di cui si parla nel testo dell'esercizio è assimilabile ad una bobina rettangolare che si sta muovendo con velocità v attraverso un campo magnetico perpendicolare al piano della bobina stessa.
A tale bobina è collegato un condensatore C:
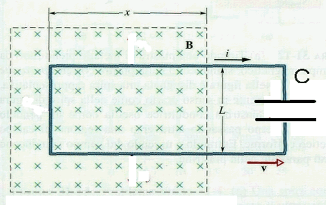
I dati forniti dal problema sono:
L = 20 cm = 0,2 m
B = 0,5 T
v = 2 m/s
S = 100 cm2 = 100 · 10-4 m2 = 10-2 m2
d = 0,5 cm = 0,5 · 10-2 m
Poiché la bobina si sta muovendo all'interno di un campo magnetico, per la legge di Faraday-Neumann la variazione di flusso del campo magnetico attraverso la superficie del circuito provoca una corrente indotta.
E se è presente una corrente, sarà anche presente appunto una tensione indotta:
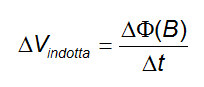
Ricordando che il flusso del campo magnetico è definito come:
Φ(B) = S · B · cosα
in cui
S è la superficie di cui si deve calcolare il flusso del campo
B è l'intensità del campo magnetico
α è l'angolo che la direzione di B forma con la direzione perpendicolare alla superficie,
si ha che:
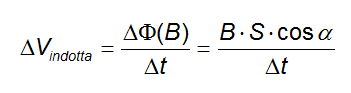
Ora la superficie attraverso la quale calcolare il flusso è quella del piano del circuito e dunque l'angolo tra la normale a questa superficie e il campo vale 0.
La superficie spazzata è il prodotto del lato L del circuito per la distanza orizzontale x percorsa, per cui:
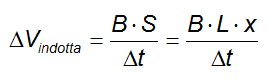
Ma il rapporto tra x e la variazione di tempo non rappresenta altro che la velocità orizzontale v con cui la barretta si sta muovendo all'interno del campo:
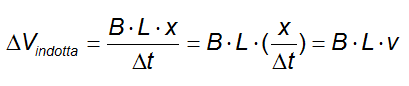
E ricordando che all'interno di un condensatore vale la relazione tra campo elettrico e potenziale:
E = V/d
Otterremo:
E = ∆Vindotta /d = B · L · v / d = 0,5 · 0,2 · 2 / (0,5 · 10-2) = 40 V/m
Ricordando la definizione di capacità come rapporto tra la carica che si deposita sulle armature e tensione:
C = Q/∆V
e che la capacità è pari a:
C = ε0 · S/d
in cui S è la superficie e d la distanza tra le armature; otteniamo:
Q = C ·∆Vindotta = (ε0 · S/d) ·∆Vindotta
Sostituendo i dati in nostrompossesso, si ha che:
Q = 8,99 · 10-12 ·10-2 / (0,5 · 10-2) ·(0,5 · 0,2 · 2 ) = 3,5 pC (picocoulomb)
Per cui il campo elettrico nel condensatore vale 40 V/m mentre la carica vale 3,5 pC.
Studia con noi