Esercizio su circuito RC
Esercizio svolto su circuito RC
Il funzionamento di una luce ad intermittenza è regolato da un circuito RC che ne determina l'intervallo di tempo occorrente tra circuito aperto e chiuso e quindi tra l'illuminarsi o meno della lampada.
Tale circuito RC è costituito da un resistore da 5,00 MΩ e da un condensatore da 2,50 μF, inizialmente scarico.
Il circuito viene così connesso ad una semplice batteria a 12 V.
Calcolare:
- la carica iniziale sul condensatore
- la corrente nel circuito dopo che è passato un periodo di tempo pari a τ
- dopo quanto tempo dalla connessione alla batteria, la ddp sul condensatore raggiunge il valore di 5,50 V.
Svolgimento
Il circuito presentato dal problema è di tipo RC, ovvero un circuito costituito da una resistenza R ed un condensatore di capacità C connessi in serie tra di loro e collegati ad un generatore di tensione:
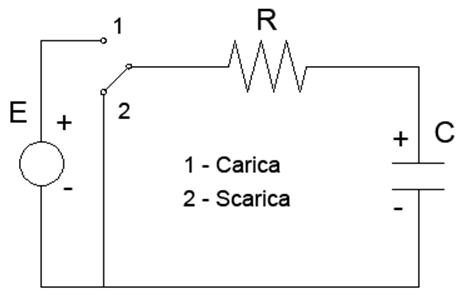
Nella figura sopra è stata riportata la situazione fisica.
All'inizio condensatore e resistenza non sono collegati al generatore di tensione.
Ad un certo momento si chiude il circuito e quindi inizia il processo di carica del circuito.
I dati sono i seguenti:
R = 5,00 MΩ = 5,00 · 106 Ω
C = 2,50 μF = 2,50 10-6 F
V0 = 12 V
Nel momento iniziale, cioè quanto t = 0 la carica sul condensatore è nulla, in quanto il circuito è aperto e non collegato ad alcun generatore.
Una volta chiuso il circuito, resistenza e condensatore risulteranno connessi alla batteria e tensione e corrente sono adesso elementi variabili nel tempo secondo le relazioni:
V(t) = V0 · (1 - e-t/τ)
i(t) = V0 /R · e-t/τ
in cui τ è detta costante di tempo e vale
τ = R · C
Dunque la corrente dopo che è trascorso un tempo pari a τ vale:
i(τ) = V0 /R · e-t/τ = V0 /R · e- τ /τ = V0 /R · e-1 = V0 /(e · R)
Sostituendo i dati in nostro possesso si ha che:
i(τ) = 12/ (2,718 · 5,00 · 106) = 8,8 · 10-7 A
Infine ricaviamo quanto tempo è trascorso dopo che viene rilevata una ddp di 5,50 V sulle armature del condensatore.
Sappiamo che:
V(t) = V0 · (1 - e-t/τ) = 5,50
Ricaviamo t:
1 - e-t/τ = 5,50 / V0
e-t/τ = 1 - 5,50 / V0
- t/ τ = ln ( 1 - 5,50/ V0 )
t = - τ · ln ( 1 - 5,50/ V0 ) = - R · C · ln ( 1 - 5,50/ V0 )
Sostituendo i dati in nostro possesso si ha che:
t = - 5,00 · 106 · 2,50 10-6 · ln (1 - 5,50/12) = 7,66 s
Ricapitolando dunque:
- la carica iniziale sul condensatore vale zero Q = 0
- la corrente nel circuito dopo che è passato un periodo di tempo pari a τ è 8,8 · 10-7 A
- la ddp sul condensatore raggiunge il valore di 5,50 V dopo un periodo di tempo pari a 7,66 s.
Link correlati:
Collegamento di due o più condensatori in serie
Studia con noi