Esercizio sulla capacità di un condensatore
Esercizio svolto sulla capacità di un condensatore
Un condensatore piano possiede le piastre di forma circolare ed ha capacità pari a 1 μF.
Nell'ipotesi che ci sia aria tra le due armature e che queste distino 2 mm, determinare il raggio di ogni armatura.
Svolgimento
Scriviamo i dati del problema:
C = 1 μF = 10-6 F
d = 2 mm = 2 · 10-3 m
Il condensatore sarà dunque di questo genere:
Il nostro obiettivo è quello di determinare il raggio di un'armatura.
Come noto, la capacità di un condensatore non dipende dalla carica presente sulle armature ma dalla geometria del condensatore stesso, in particolare:
C = ε0 · S/d
in cui
- ε0 è la costante dielettrica relativa nel vuoto e vale 9 · 10-12 C2/(N · m2)
- S è la superficie delle armature
- d la distanza tra esse.
Poiché la forma geometrica delle armatura è di tipo circolare, ricordiamo che l'area di un cerchio si calcola come:
S = π · R2
in cui R è proprio il raggio dell'armatura.
Dunque avremo:
C = ε0 · S/d = ε0 · π · R2/d
Ricaviamo R dalla formula inversa:
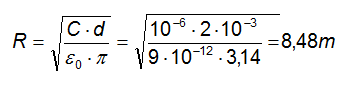
Dunque per avere un condensatore con queste caratteristiche capacitive, il raggio di ogni armatura deve essere pari a 8,48 m.
Ciò conferma che il Farad è in realtà un'unità di misura molto grande, viste le dimensioni dell'armatura.
Link correlati:
Esercizio sul calcolo della carica depositata su un condensatore
Come avvengono la carica e la scarica di un condensatore?
Studia con noi