Moto rettilineo uniformemente accelerato
Studio del moto rettilineo uniformemente accelerato
In generale il moto rettilineo è vario, nel senso che la velocità varia nel tempo secondo leggi e relazioni diverse.
Se un moto vario è caratterizzato da accelerazione costante, ovvero la velocità cresce o descresce sempre della stessa quantità ogni secondo, allora si parla di moto rettilineo uniformemente accelerato.
Legge velocità - tempo
La velocità è legata al tempo tramite una relazione lineare rispetto al tempo, ovvero una relazione di primo grado di questo tipo:
![]()
in cui
- a è l'accelerazione costante espressa in m/s2
- t il tempo espresso in s
- V0 l'eventuale velocità iniziale al tempo t = 0
Dalla precedente si ricavano tutte le formule inverse:
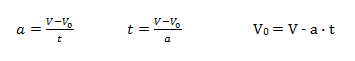
Legge oraria del moto rettilineo uniformemente accelerato
La legge oraria di un moto rettilineo uniforme, ovvero l'equazione che lega la posizione al tempo, è del tipo:
![]()
in cui
S0 rappresenta lo spazio iniziale al tempo t = 0.
Come è possibile notare dalla precedente equazione, lo spazio è legato al tempo tramite una relazione quadratica, ovvero di secondo grado.
Relazione spazio - velocità
È possibile legare tra loro in un'unica formula spazio e velocità senza ricorrere alla variabile tempo.
Questa formula è molto utile in una grande quantità di problemi dove appunto non si conosce il tempo.
Poniamo per semplicità S0 = 0 e leghiamo le due formule citate sopra:
V(t) = a ∙ t + V0
e
S(t) = ½ ∙ a ∙ t2 + V0 ∙ t
In particolare esplicitiamo il tempo t dalla prima e sostituiamolo nella seconda:
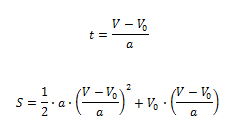
Eseguendo i calcoli otteniamo:
![]()
Da questa si ricavano le formule inverse:
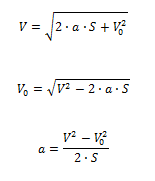
ed infine:
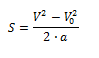
Grafico velocità - tempo
Il grafico velocità tempo di un moto rettilineo uniformemente accelerato, essendo la relazione che lega velocità e tempo di tipo lineare, sarà una retta che intercetta l'asse y in corrispondenza del valore di V0.
Ad esempio, nel caso in cui un corpo si muova con accelerazione costante pari a 0,5 m/s2 e che la velocità iniziale sia pari a -2 m/s il grafico velocità tempo sarà di questo tipo:
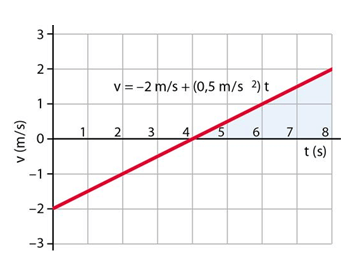
La velocità è inizialmente negativa mentre l'accelerazione è positiva.
Quindi il corpo si sta inizialmente muovendo verso la parte negativa del sistema di riferimento scelto, rallentando fino a fermarsi e ad invertire il proprio moto al tempo t=4 in cui la velocità si annulla ed inizia ad incrementarsi assumendo valori positivi.
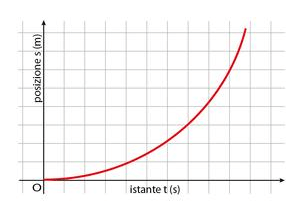
Grafico spazio - tempo nel moto rettilineo uniformemente accelerato
Il grafico spazio tempo invece sarà un ramo di parabola, essendo la relazione che lega spazio e tempo di tipo quadratico:
Moto rettilineo uniformemente ritardato
Quando l'accelerazione è negativa (a < 0) e quindi il corpo subisce un decremento della propria velocità, il moto si definisce "ritardato" o "decelerato".
Le due leggi, velocità - tempo e spazio - tempo appena viste, assumeranno la forma del tipo:
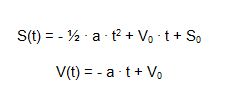
I grafici saranno i medesimi come nel caso a > 0 ma con la differenza che il grafico velocità tempo sarà una retta con pendenza decrescente
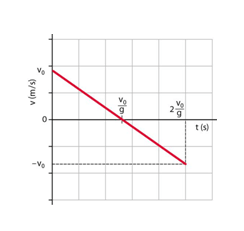
mentre il grafico spazio tempo sarà una parabola con concavità rivolta verso il basso:
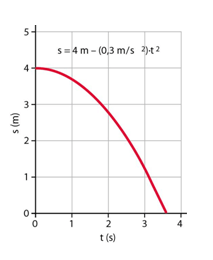
Esempio
Dalla scheda tecnica di due automobili di diversa cilindrata si legge che il tempo per passare da 0 a 100 km/h è di 5 s per la prima e di 8 s per la seconda.
Calcolare il valore dell'accelerazione media per entrambe.
Quanto vale lo spazio percorso nei due casi?
E la velocità media di ognuno?
Lo svolgimento dell'esercizio lo trovi qui: calcolo della accelerazione media.
Esercizi sul moto rettilineo uniformemente accelerato
Se ti interessano li trovi qui: esercizi moto rettilineo uniformemente accelerato.
Link correlati:
Quali sono le formule del moto rettilineo uniformemente accelerato?
Quali sono le formule inverse della accelerazione?
Esercizi svolti e commentati sulla caduta dei gravi
Quali sono le formule della caduta libera?
Che cos'è e come avviene il moto rettilineo uniforme?
Che cos'è e come avviene il moto circolare uniforme?
Come calcolare l'accelerazione nel moto rettilineo uniformemente accelerato
Che cos'è l'accelerazione?
Esercizio su un sasso lanciato verso l'alto
Studia con noi