Equazioni di Maxwell
Cosa affermano le equazioni di Maxwell?
Nel 1873 il fisico scozzese James Clerk Maxwell pubblica il Trattato sull'elettromagnetismo (Treatise on Electricity and Magnetism) in cui espone un'unica teoria che sulla base di quattro equazioni perfettamente simmetriche tra di loro è capace di descrivere allo stesso tempo tutti i fenomeni elettrici e magnetici, che fino ad allora si pensava facessero parte di due diverse branche della fisica.
Le quattro equazioni esposte da Maxwell sono leggi e teoremi precedentemente scritte da altri fisici ma che opportunamente combinate tra di loro porteranno alla scoperta di un nuovo importante fenomeno quello delle onde elettromagnetiche.
Maxwell inoltre provvederà ad integrare una di queste quattro equazioni (il teorema di Ampere) con una parte mancante e che esporremo tra poco.
Le quattro equazioni di Maxwell sono:
- teorema di Gauss per il campo elettrico
- teorema di Gauss per il campo magnetico
- circuitazione del campo elettrico (legge di Faraday Neumann Lenz)
- circuitazione del campo magnetico (teorema di Ampere - Maxwell)
Prima equazione di Maxwell: teorema di Gauss per il campo elettrico
Il teorema di Gauss per E afferma che il flusso del campo elettrico attraverso una superficie chiusa è pari alla somma algebrica delle cariche interne alla superficie divisa per la costante dielettrica nel vuoto ε0 :
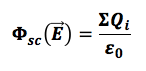
ricordando che ε0 = 8,85 ∙10-12 N∙m2/C2.
Il significato fisico della prima equazione di Maxwell, cioè del teorema di Gauss per il campo elettrico, è il seguente:le sorgenti del campo elettrostatico sono le cariche elettriche; le linee di campo sono linee aperte che si originano dalle stesse cariche e vanno verso l'infinito nel caso di cariche positive (dette sorgenti) oppure provengono dall'infinito e terminano sulla carica nel caso di cariche negative (dette pozzi).
Dal teorema di Gauss discendono tutte le proprietà relative al campo elettrico ed ai fenomeni elettrici come il teorema di Coulomb, il potenziale elettrico, ecc.
Seconda equazione di Maxwell: teorema di Gauss per il campo magnetico
Il teorema di Gauss per B afferma che il flusso del campo magnetico attraverso una qualsiasi superficie chiusa è sempre pari a zero:
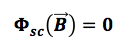
Il significato fisico della seconda di equazione di Maxwell, cioè del teorema di Gauss per il campo magnetico è il seguente:le linee di campo magnetico sono sempre linee chiuse, si originano nel polo nord di un magnete e convergono verso il polo sud. Non è inoltre possibile separare tra di loro i due poli cioè non è possibile realizzare un monopolo magnetico.
Il fatto che le linee di campo magnetico siano sempre chiuse determina la proprietà del campo magnetico di essere un campo non conservativo a differenza del campo elettrostatico che invece lo è.
Per parlare della terza e della quarta equazione di Maxwell è bene distinguere due casi. Il caso in cui i campi siano statici e quello in cui invece essi siano variabili. Vedremo come l'equazione nel caso statico non sia altro che un caso particolare dell'equazione espressa in forma più generale nel caso variabile.
Terza equazione di Maxwell: circuitazione del campo elettrico
Ripassiamo velocemente cosa si intende per circuitazione di un campo vettoriale e poi vediamo il risultato della circuitazione applicata al campo elettrico nei due casi statico e variabile cioè la terza equazione di Maxwell.
Consideriamo un campo elettrostatico E ed una linea chiusa orientata L di cui si stabilisce il verso di percorrenza.
Immaginiamo di dividere la linea L in un numero n molto elevato di piccoli tratti ognuno di lunghezza Δl1, Δl2, Δl3 ... Δln in modo da poter considerare il campo elettrico uniforme E1, E2, E3, ... En, per ogni tratto infinitesimo.
Associamo ad ogni tratto Δl il relativo vettore spostamento Δl1, Δl2, Δl3, ... Δln, associato al movimento lungo la linea orientata.
Si definisce circuitazione di E lunga la linea L la somma di tutti i prodotti scalari tra ogni vettore campo elettrico misurato nell'i-esima parte in cui è stata suddivisa la linea e il relativo vettore spostamento:
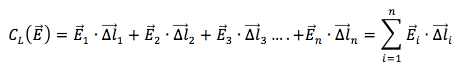
1) caso statico
Per un campo elettrostatico la circuitazione lungo un percorso chiuso L vale zero ovvero è nulla:
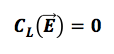
Il significato fisico della terza equazione di Maxwell nel caso statico è che il campo elettrostatico è un campo conservativo, ovvero il lavoro svolto dalle forze del campo non dipende dal cammino percorso ma soltanto dalla posizione iniziale e da quella finale ed in particolare se posizione iniziale e finale coincidono (percorso chiuso) allora il lavoro è nullo.
2) caso variabile
In presenza di campi variabili la terza equazione di Maxwell assume l'aspetto più generale e sempre valido:
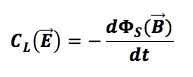
Questa equazione rappresenta la legge di Faraday Neumann Lenz dell'induzione elettromagnetica infatti la circuitazione del campo elettrico rappresenta la forza elettromotrice così come nell'espressione originale della legge in questione.
In particolare la circuitazione del campo elettrico lungo una linea chiusa L è pari alla derivata del flusso del campo magnetico concatenato alla superficie racchiusa dalla linea L rispetto al tempo cambiato di segno (legge di Lenz).
Il fatto che compaia la derivata è perché si tratta di variazione di grandezze istantanee altrimenti in maniera più approssimativa sostituibile con il Δ per ottenere una fem media e non istantanea. Il significato fisico nell'ottica di una teoria unificata dell'elettromagnetismo è che un campo magnetico variabile nel tempo è sorgente di un campo elettrico indotto non conservativo cioè con circuitazione non nulla.
Quarta equazione di Maxwell: circuitazione del campo magnetico
Ripassiamo velocemente cosa si intende per circuitazione di un campo vettoriale e poi vediamo il risultato della circuitazione applicata al campo magnetico nei due casi statico e variabile cioè la quarta equazione di Maxwell.
Consideriamo un campo magnetico B ed una linea chiusa orientata L di cui si stabilisce il verso di percorrenza.
Immaginiamo di dividere la linea L in un numero n molto elevato di piccoli tratti ognuno di lunghezza Δl1, Δl2, Δl3 ... Δln in modo da poter considerare il campo elettrico uniforme B1, B2, B3, ... Bn, per ogni tratto infinitesimo.
Associamo ad ogni tratto Δl il relativo vettore spostamento Δl1, Δl2, Δl3, ... Δln, associato al movimento lungo la linea orientata.
Si definisce circuitazione di B lunga la linea L la somma di tutti i prodotti scalari tra ogni vettore campo magnetico misurato nell'i-esima parte in cui è stata suddivisa la linea e il relativo vettore spostamento:
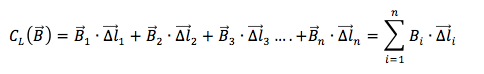
1) caso statico
La circuitazione del campo magnetico lungo una linea chiusa e orientata L in assenza di campi elettrici variabili è pari al prodotto della permeabilità magnetica nel vuoto μ0 per la somma algebrica di tutte le correnti concatenate al percorso, cioè solo quelle correnti elettriche che attraversano la superficie racchiusa dalla linea L
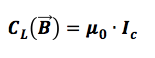
Questa legge è nota come Teorema di Ampere e da questa legge, ad esempio, discende il calcolo dell'intensità di un campo magnetico generato da un filo percorso da corrente (legge di Biot Savart).
2) caso variabile
Maxwell si accorse che quando si considerano anche i campi elettrici variabili la legge della circuitazione di Ampere risultava incompleta di qualcosa. Infatti consideriamo un circuito in cui è presente un condensatore e scegliamo un percorso chiuso di forma circolare attorno al filo di conduzione in cui scorre la corrente ic:
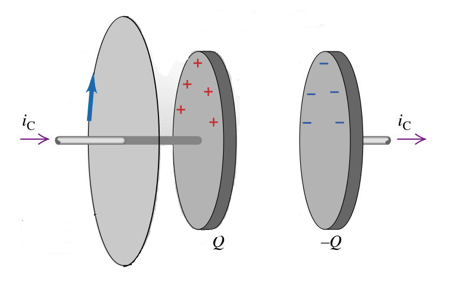
Applichiamo il teorema di Ampere a questo percorso circolare. L'unica corrente concatenata al percorso è ic e pertanto la circuitazione del campo magnetico generato dal filo che trasporta corrente è
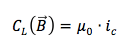
Ora scegliamo una forma della linea più complessa con contorno sempre pari a L però per cui la superficie risulta essere posta tra le armature del condensatore:
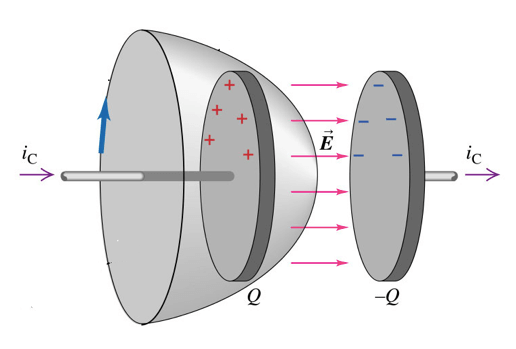
In questo caso nessuna corrente di conduzione risulta oltrepassare la superficie racchiusa dalla linea in quanto tra i condensatori non circolare corrente essendo le due armature separate da un dielettrico e quindi otterremmo una circuitazione nulla del campo magnetico:
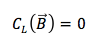
Si arriva cioè a una contraddizione ovvero a un paradosso per cui la circuitazione lungo la curva L non può avere due valori diversi se applicato allo stesso campo magnetico.
Maxwell allora fece questo ragionamento: in realtà la carica di un condensatore non è istantanea. Man mano che circola corrente nel filo allora si depositerà una carica sempre più crescente nelle armature del condensatore le cui piastre si caricano entrambe con la stessa quantità di carica ma cambiata di segno per induzione. Man mano che la carica si deposita sulle piastre ed aumenta fino a saturare il condensatore il campo elettrico tra le armature aumenta essendo esso uniforme e pari al rapporto tra la densità superficiale di carica e la costante dielettrica nel vuoto:
E = σ / ε0
Dunque durante la fase di carica del condensatore bisogna considerare che tra le armature si genera un campo elettrico variabile il cui flusso sarà anch'esso variabile.
Allora Maxwell aggiunse al teorema della circuitazione di Ampere un termine mancante detto corrente di spostamento che era pari al prodotto della costante dielettrica nel vuoto per la derivata rispetto al tempo del flusso del campo elettrico calcolato attraversato la superficie racchiuso dalla linea circuitale L:
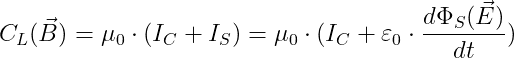
Il teorema da allora assunse il nome di Teorema di Ampere – Maxwell e il termine di corrente di spostamento fu detto così perché ha le dimensioni dell'Ampere.
Il significato fisico che assume allora questa quarta equazione è che: le sorgenti del campo magnetico sono le correnti di conduzione o i campi elettrici variabili nel tempo.
Link correlati:
Che cos'è la densità di corrente elettrica?
Qual è l'unità di misura della corrente di spostamento?
Esercizio svolto sulla legge di Hopkinson
Che cos'è l'effetto Hall?
Cosa afferma la legge di Hopkinson?
Che cos'è la riluttanza?
Studia con noi