Accelerazione centripeta
Come si calcola l'accelerazione centripeta?
In un moto curvilineo il vettore velocità cambia posizione istante per istante, se poi il moto è di tipo non uniforme allora varierà anche il modulo:
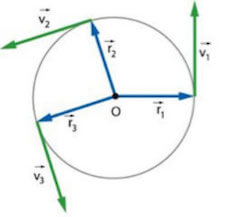
Poiché; il vettore velocità subisce variazione allora siamo in presenza di accelerazione.
Possono esistere due tipi di accelerazioni in un moto circolare, l'accelerazione centripeta e l'accelerazione tangenziale.
L'accelerazione tangenziale interviene quando il modulo della velocità tangenziale varia, aumenta o decrementa. Se invece, come nel caso nel moto circolare uniforme, la velocità tangenziale si mantiene costante allora l'accelerazione tangenziale vale zero.
L'accelerazione centripeta (centripeta vuol dire che è diretta verso il centro ) è invece un vettore che risulta perpendicolare al vettore velocità e rivolto lungo la stessa direzione del raggio verso il centro della circonferenza:
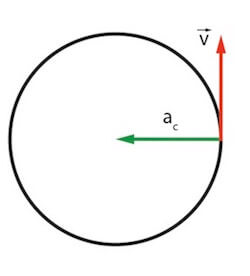
Valore dell'accelerazione centripeta in un moto circolare uniforme
Per calcolare il valore del modulo del vettore accelerazione centripeta chiamiamo Δs la distanza percorsa lungo un arco da un punto materiale che si sta muovendo di moto circolare uniforme e Δt il tempo occorso a percorrere questo arco:
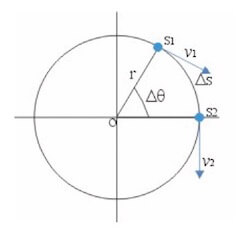
L'angolo spazzato in tale istante di tempo sarà dato (in radianti):
Δθ = Δs/r (per definizione di angolo al centro come rapporto tra la lunghezza dell'arco Δs ed il raggio r della circonferenza).
Allora l'arco percorso vale:
Δs = Δθ · r
La velocità è data dal rapporto tra distanza percorsa e tempo impiegato a percorrerla; inoltre essendo il moto di tipo uniforme essa sarà costante:
v = Δs/Δt = Δθ · r / Δt
Immaginiamo ora il punto che sta ruotando e quindi passa dalla velocità v1 a v2; calcoliamo la variazione delle velocità Δv
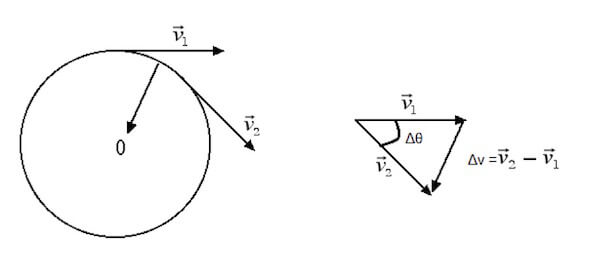
Essendo il moto circolare uniforme i vettori v1 e v2 hanno lo stesso modulo che chiamiamo per semplicità v.
Dunque il triangolo che per lati v1, v2, Δv è un triangolo isoscele di base Δv.
Applichiamo il teorema di Carnot per calcolare il valore di Δv:
Δv2= v12 + v22 - 2 · v1 · v2 · cos(Δθ)
Essendo v1 = v2= v (modulo della velocità tangenziale):
Δv2= v2 + v2 - 2 · v · v · cos(Δθ) = 2 · v2 - 2 · v2 · cos(Δθ) = v2 · [2 - 2 · cos(Δθ)]
Dividiamo per v2 :
Δv2/ v2 = [2 - 2 · cos(Δθ)] = 2 [1 - cos(Δθ)]
Moltiplichiamo e dividiamo il secondo membro per [1 + cos(Δθ)] così da non alternarne la sostanza:
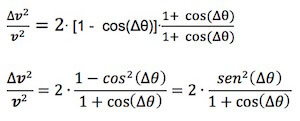
Ora poiché; vogliamo conoscere il valore dell'accelerazione istantanea, facciamo tendere l'angolo spazzato ad un infinitesimo per poter conoscere il comportamento in un istante di tempo molto piccolo:
Δθ→0
Il termine sen(Δθ), per Δθ→0, diventa proprio l'angolo Δθ, ovvero il seno si può tranquillamente approssimare col suo argomento, mentre il termine [1 + cos(Δθ)] tende a 2 in quanto cos0 = 1.
Dunque estraendo la radice quadrata di ambo i membri otteniamo:
|Δv|/v ≈ Δθ = Δs/r
che possiamo scrivere come:
|Δv| ≈ v · Δs/r
L'accelerazione è definita come il rapporto tra variazione di velocità e variazione di tempo:
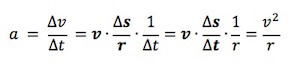
Dunque, l'accelerazione centripeta è data dal rapporto tra il quadrato della velocità tangenziale e il raggio della circonferenza.
In un moto circolare uniforme l'accelerazione centripeta rimane costante.
Formule per calcolare l'accelerazione centripeta
Partendo dalla formula
ac = v2/r
ricaviamo le due formule inverse:
r = v2 / ac
e
![]()
Combinando infine le formule dell'accelerazione centripeta con le altre del moto circolare uniforme otteniamo:

accelerazione centripeta e moto vario
Se il modulo della velocità tangenziale non è più costante allora il punto subisce un'accelerazione tangenziale oltre essere soggetto all'accelerazione centripeta.
Le due accelerazioni hanno però funzioni diverse: quella tangenziale è la causa della variazione della velocità mentre quella centripeta è la causa della variazione della direzione istante per istante del vettore velocità.
Il modulo dell'accelerazione centripeta è sempre pari a:
ac = v2/r
in questo caso però essa dipende dalla velocità tangenziale
Esercizio sulla accelerazione centripeta
Un satellite artificiale in orbita attorno alla Terra è soggetto ad un'accelerazione centripeta di 9,8 m/s2.
Qual è la velocità tangenziale ed il periodo dell'orbita?
PS Approssimare il raggio dell'orbita a 6371 km (pari al valore del raggio della Terra)
La soluzione dell'esercizio la trovi qui: calcolo della velocità tangenziale.
Esercizio sulla velocità tangenziale
L'addestramento degli astronauti destinati ai viaggi spaziali verso la stazione orbitante prevedono delle simulazioni di aumento dell'accelerazione di gravità.
Ad esempio, durante la fase di discesa del velivolo sulla Terra proveniente dallo spazio, a causa della presenza dell'atmosfera terrestre, la velocità può passare bruscamente anche da 8000 m/s a 300 m/s.
Gli astronauti pertanto potrebbero essere sottoposti ad accelerazioni di gravità fino a 8g.
Per simulare questa situazione critica, si utilizza un braccio rotante di circa 18 m posto in velocità costante e al cui estremo è presente un fissaggio a cui risulta ancorato l'astronauta.
Determinare a che velocità deve ruotare il braccio affinché; la simulazione avvenga correttamente e quanti giri compie in un minuto.
La soluzione dell'esercizio la trovi qui: esercizio sulla velocità tangenziale.
Studia con noi