Esercizio sull'equilibrio di un corpo rigido
Esercizio svolto sull'equilibrio di un corpo rigido
Una scala, la cui forza peso è 69 N, è appoggiata ad una parete liscia.
Sulla scala è presente un uomo, forza peso di 490 N, che si trova esattamente a tre quarti della lunghezza della stessa.
Sapendo che la scala forma un angolo di 60° con la superficie scabra del pavimento, calcolare l'intensità della forza di attrito che esiste tra scala e pavimento.
Svolgimento dell'esercizio
Facciamo un disegno della situazione statica, disegnando tutte le forze coinvolte:
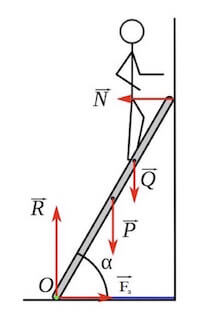
La scala è poggiata ai due suoi estremi, uno al pavimento che chiamiamo O e che consideriamo come polo, e l'altro estremo alla parete verticale.
Pertanto ad ognuno di questi due estremi sarà presente una reazione vincolare, perpendicolare alla superficie di appoggio, che chiamiamo rispettivamente R ed N.
Consideriamo ora le forze peso: quella della scala la consideriamo in corrispondenza del suo centro di massa (baricentro) e la chiamiamo P, quella dell'uomo sarà invece presente ai ¾ della lunghezza e la chiamiamo Q.
Infine è presente la forza di attrito Fa diretta lungo l'asse orizzontale, in verso opposto a quello che sarebbe il moto di naturale scivolamento della scala verso sinistra.
Calcoliamo ora le distanze di tutte le forze dal polo O, ovvero calcoliamo la misura del braccio di ogni forza.
Il braccio di R e Fa è nullo.
Il braccio di P è pari a (L/2) e il vettore forma con la scala un angolo di 30° (in quanto se si considera il triangolo rettangolo formato da mezza scala, un cateto verticale pari al prolungamento del vettore P in figura e cateto orizzontale la distanza tra O e il punto in cui il cateto verticale incontra il pavimento, allora se α è 60 ° l'altro angolo necessariamente deve essere 30° in quanto la somma degli angoli interni di un triangolo è sempre 180°); quello di Q invece (¾)∙L ed il vettore forma un angolo di 30° con la direzione del braccio.
Infine il braccio della forza N è L e l'angolo col braccio vale 60°.
Poiché siamo in condizioni statiche, per l'equilibrio di un corpo rigido deve accadere che la somma di tutti i momenti calcolati rispetto a O deve essere nulla; pertanto:
P ∙ (L/2) ∙ sen30 + Q ∙ (¾) ∙ L ∙ sen30 – N ∙ L ∙ sen60 = 0
Il momento di N è negativo in quanto i primi due hanno momento entrante nel foglio (secondo la regola della mano destra), mentre esso ha momento uscente.
Quindi, secondo il sistema di riferimento adottato, i primi due hanno verso positivo mentre l'ultimo verso negativo.
Nulla cambiava se la sequenza dei segni era negativo e negativo per i primi due, positivo per l'ultimo.
Possiamo semplificare L nella precedente:
P∙(½)∙sen30 + Q ∙ (¾) ∙ sen30 – N ∙ sen60 = 0
N ∙ sen60 = P ∙ (½) ∙ sen30 + Q ∙ (¾) ∙ sen30
N = [P∙ (½) ∙ sen30 + Q ∙ (¾) ∙ sen30]/sen60
N = [69 ∙ (½) ∙ sen30 + 490 ∙ (¾) ∙ sen30]/sen60 = 230 N
Ora poiché le uniche due forze orizzontale sono la reazione N della parete e la forza di attrito Fa, allora sempre l'equilibrio avremo:
∑ Fest,x = 0
Pertanto:
Fa – N = 0
Fa = N = 230 N
Dunque la forza di attrito tra la scala ed il pavimento vale 230 N.
Studia con noi